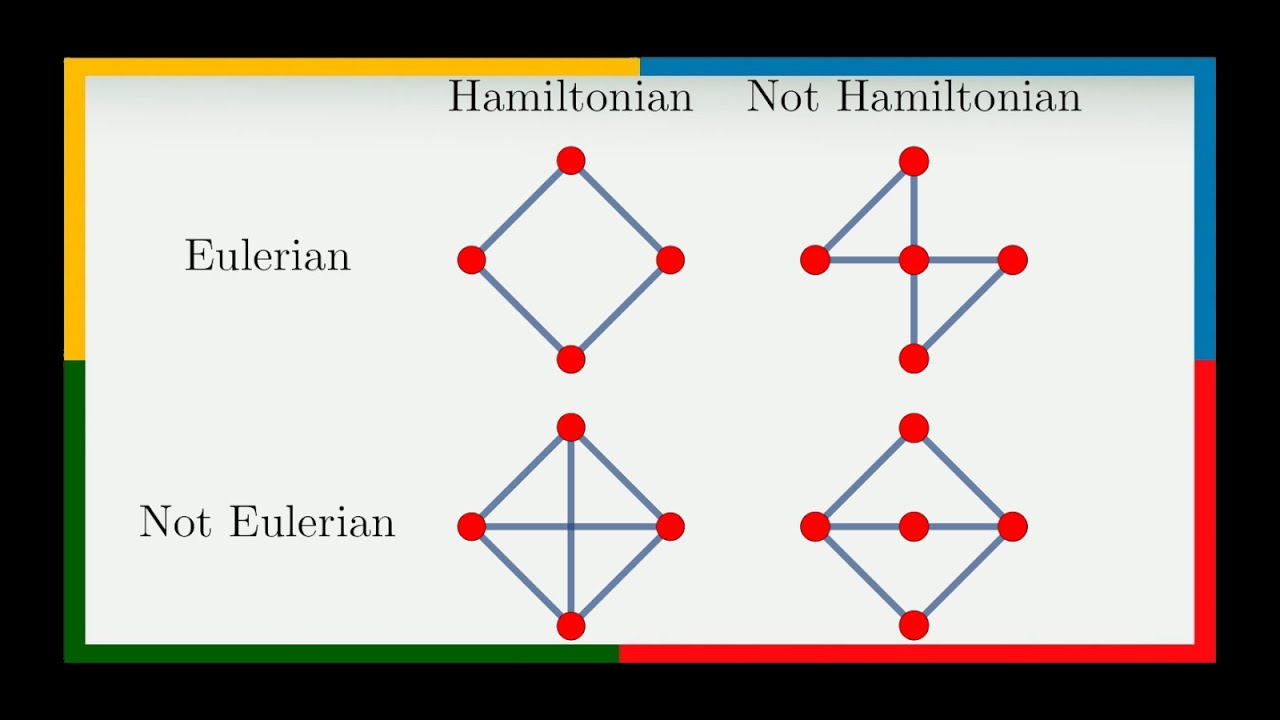
Hamilton graphs are a fascinating topic in mathematics, especially in graph theory. Named after the mathematician Sir William Rowan Hamilton, these graphs have a unique property: they contain a Hamiltonian cycle, a path that visits each vertex exactly once and returns to the starting point. But what makes Hamilton graphs so intriguing? Understanding Hamilton graphs can help solve complex problems in computer science, logistics, and network design. They are not just theoretical constructs; they have practical applications in real-world scenarios. From optimizing delivery routes to designing efficient circuits, Hamilton graphs play a crucial role. Ready to dive into 27 mind-blowing facts about Hamilton graphs? Let's get started!
What Are Hamilton Graphs?
Hamilton graphs are a fascinating concept in graph theory. Named after the mathematician Sir William Rowan Hamilton, they have unique properties that make them a favorite topic among mathematicians and computer scientists.
- A Hamilton graph contains a Hamiltonian cycle, which is a cycle that visits each vertex exactly once and returns to the starting vertex.
- The concept was inspired by Hamilton's 1857 puzzle, the Icosian Game, which involved finding a Hamiltonian cycle on a dodecahedron.
- Not all graphs are Hamiltonian. Determining whether a given graph is Hamiltonian is an NP-complete problem, meaning it is computationally challenging.
- A Hamiltonian path is similar to a Hamiltonian cycle but does not require returning to the starting vertex.
- The Traveling Salesman Problem (TSP) is a famous problem in computer science that involves finding the shortest Hamiltonian cycle in a weighted graph.
Properties of Hamilton Graphs
Understanding the properties of Hamilton graphs can help in identifying and working with them. These properties often reveal the underlying structure and complexity of the graph.
- A Hamiltonian graph is always connected, meaning there is a path between any two vertices.
- Dirac's theorem states that a graph with ( n ) vertices (where ( n geq 3 )) is Hamiltonian if every vertex has a degree of at least ( n/2 ).
- Ore's theorem extends Dirac's theorem by stating that a graph is Hamiltonian if the sum of the degrees of any two non-adjacent vertices is at least ( n ).
- A Hamiltonian graph can be both planar and non-planar. Planar graphs can be drawn on a plane without edges crossing.
- The Petersen graph is a famous example of a non-Hamiltonian graph, despite being 3-regular and having 10 vertices.
Applications of Hamilton Graphs
Hamilton graphs have practical applications in various fields, from logistics to biology. Their unique properties make them useful for solving real-world problems.
- In logistics, Hamiltonian cycles can optimize routes for delivery trucks, reducing travel time and fuel consumption.
- In biology, Hamiltonian paths can model the sequence of genetic mutations or the spread of diseases.
- In telecommunications, Hamiltonian cycles can optimize the layout of network circuits to ensure efficient data transmission.
- In robotics, Hamiltonian paths help in planning the movement of robots to cover an area without retracing steps.
- In computer graphics, Hamiltonian cycles can be used to generate efficient rendering paths for complex scenes.
Famous Hamilton Graphs
Several well-known graphs are Hamiltonian, each with unique characteristics that make them interesting to study.
- The complete graph ( K_n ) is Hamiltonian for any ( n geq 3 ). In a complete graph, every pair of distinct vertices is connected by a unique edge.
- The dodecahedron graph, which has 20 vertices and 30 edges, is Hamiltonian and was the basis for Hamilton's Icosian Game.
- The cube graph ( Q_n ) is Hamiltonian for any ( n geq 2 ). These graphs represent the vertices and edges of an ( n )-dimensional cube.
- The Petersen graph, despite being a counterexample to many graph theory conjectures, is not Hamiltonian.
- The Tetrahedral graph, representing the vertices and edges of a tetrahedron, is Hamiltonian.
Challenges in Hamilton Graph Theory
Hamilton graph theory poses several challenges, both in terms of theoretical understanding and practical computation.
- Determining whether a graph is Hamiltonian is NP-complete, making it computationally intensive for large graphs.
- Finding the longest Hamiltonian path in a graph is also NP-hard, adding to the complexity of working with these graphs.
- The Bondy-Chvátal theorem provides a useful condition for Hamiltonicity but is not always easy to apply.
- The problem of finding a Hamiltonian cycle can be simplified for specific types of graphs, such as bipartite or planar graphs.
- Despite the challenges, heuristic algorithms and approximation methods can often find Hamiltonian cycles in practical applications.
Fun Facts About Hamilton Graphs
Hamilton graphs are not just academically interesting; they also have some fun and quirky aspects.
- Hamilton's Icosian Game was marketed as a puzzle, making it one of the earliest examples of a mathematical concept being turned into a commercial game.
- The concept of Hamiltonian cycles has inspired numerous puzzles and games, including the popular "Knight's Tour" problem in chess, where the goal is to move a knight to every square on the board exactly once.
The Final Word on Hamilton Graphs
Hamilton graphs are fascinating. They’ve got a rich history, practical uses, and some mind-bending properties. From their origins with Sir William Rowan Hamilton to their applications in modern computer science, these graphs show how math can solve real-world problems. They’re not just theoretical; they help with things like optimizing delivery routes and network design.
Understanding Hamilton graphs can give you a new appreciation for the complexity and beauty of mathematics. They’re a perfect example of how something seemingly abstract can have concrete, impactful applications. So next time you hear about Hamilton graphs, you’ll know they’re more than just lines and points—they’re a key part of solving some of today’s toughest challenges. Keep exploring, keep questioning, and who knows? You might just find yourself solving the next big problem with a Hamilton graph.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
