28 Facts About Hill Equation

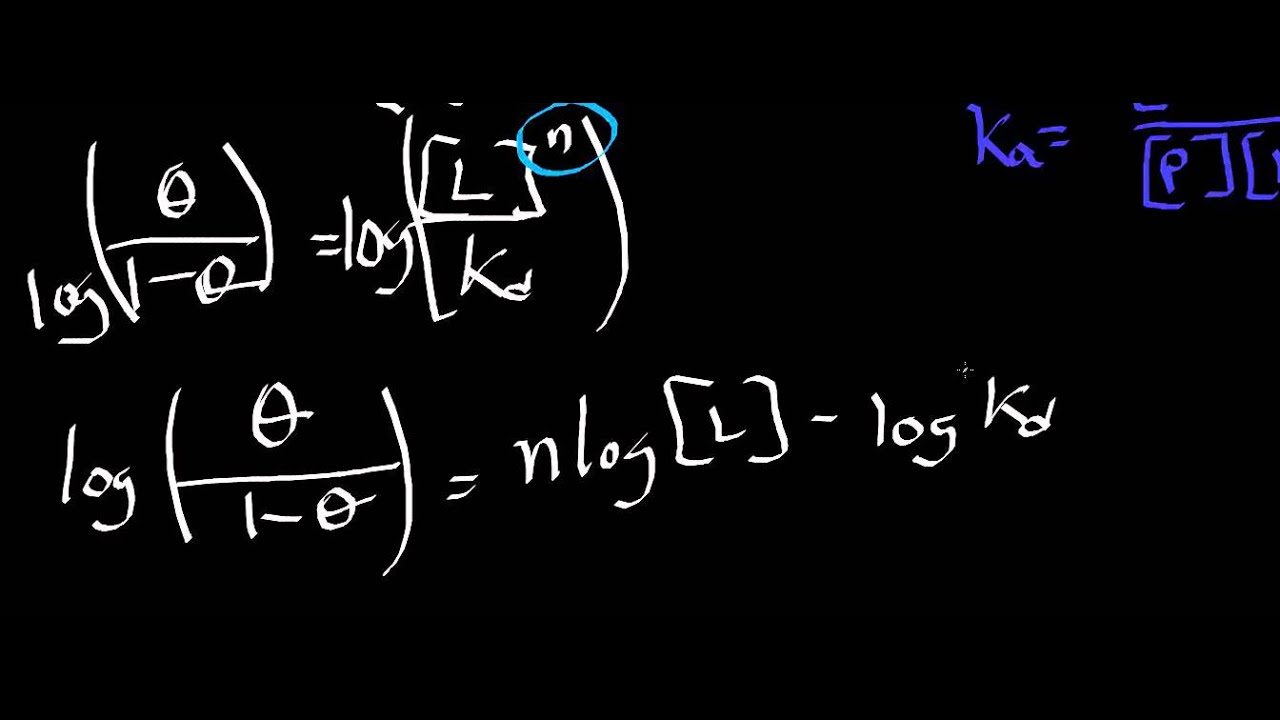
What is the Hill Equation?

The Hill equation is a mathematical formula used to describe the binding of ligands to macromolecules. It is particularly useful in biochemistry and pharmacology for understanding how drugs interact with their targets.

1. The Hill equation was first introduced by Archibald Hill in 1910.
2. It is commonly used to describe the sigmoidal (S-shaped) binding curves of hemoglobin and other proteins.
3. The equation helps in determining the cooperativity of ligand binding to a protein.
4. It is expressed as ( theta = frac{[L]^n}{K_d + [L]^n} ), where ( theta ) is the fraction of occupied binding sites, ( [L] ) is the ligand concentration, ( K_d ) is the dissociation constant, and ( n ) is the Hill coefficient.

Importance of the Hill Coefficient

The Hill coefficient, denoted as ( n ), is a crucial parameter in the Hill equation. It provides insights into the nature of ligand binding.

5. A Hill coefficient of ( n = 1 ) indicates non-cooperative binding.
6. When ( n > 1 ), it suggests positive cooperativity, meaning the binding of one ligand increases the affinity for subsequent ligands.
7. A Hill coefficient less than 1 (( n < 1 )) indicates negative cooperativity, where binding of one ligand decreases the affinity for others.
8. The Hill coefficient can also help in understanding the allosteric effects in enzymes and receptors.

Applications in Biochemistry

The Hill equation has a wide range of applications in biochemistry, particularly in the study of enzyme kinetics and receptor-ligand interactions.

9. It is used to analyze the binding of oxygen to hemoglobin.
10. The equation helps in studying the effects of various drugs on their target proteins.
11. It is also useful in understanding the binding of substrates to enzymes.
12. Researchers use the Hill equation to study the binding of hormones to their receptors.

Applications in Pharmacology

In pharmacology, the Hill equation is essential for drug development and understanding drug efficacy.

13. It helps in determining the dose-response relationship of drugs.
14. The equation is used to calculate the effective concentration (EC50) of a drug.
15. It aids in understanding the therapeutic window of medications.
16. Pharmacologists use the Hill equation to study the binding affinity of drugs to their targets.

Limitations of the Hill Equation

Despite its usefulness, the Hill equation has certain limitations that researchers should be aware of.

17. It assumes that all binding sites are identical and independent, which is not always the case.
18. The equation does not account for the effects of ligand depletion at high concentrations.
19. It may not accurately describe systems with multiple binding sites with different affinities.
20. The Hill equation is less effective for systems with complex allosteric interactions.

Historical Context and Development

Understanding the historical context of the Hill equation provides a deeper appreciation of its significance in scientific research.

21. Archibald Hill was awarded the Nobel Prize in Physiology or Medicine in 1922 for his work on muscle physiology.
22. The development of the Hill equation was influenced by earlier studies on enzyme kinetics and binding theory.
23. The equation has been modified and extended over the years to accommodate more complex binding scenarios.
24. It remains a foundational tool in biochemistry and pharmacology, despite the advent of more sophisticated models.

Modern Uses and Future Directions

The Hill equation continues to be relevant in modern scientific research, with ongoing developments and applications.

25. It is used in computational biology for modeling complex biological systems.
26. The equation is applied in the development of biosensors and diagnostic tools.
27. Researchers are exploring ways to integrate the Hill equation with machine learning algorithms for drug discovery.
28. The Hill equation remains a subject of active research, with scientists seeking to refine and expand its applications.

Final Thoughts on Hill Equation

The Hill equation is a cornerstone in biochemistry and pharmacology, helping us understand how molecules interact with each other. It's used to describe the binding of ligands to macromolecules, which is crucial for drug development and enzyme kinetics. Knowing the Hill coefficient can reveal whether a molecule binds cooperatively, which impacts how drugs are designed and used.

This equation isn't just for scientists. It has practical applications in medicine, agriculture, and even environmental science. For instance, it helps in designing more effective medications and understanding how pollutants affect ecosystems.

Understanding the Hill equation can give you a deeper appreciation for the complexities of biological systems. It's a powerful tool that bridges the gap between theoretical science and real-world applications. So next time you hear about a new drug or treatment, remember the Hill equation might be behind it.