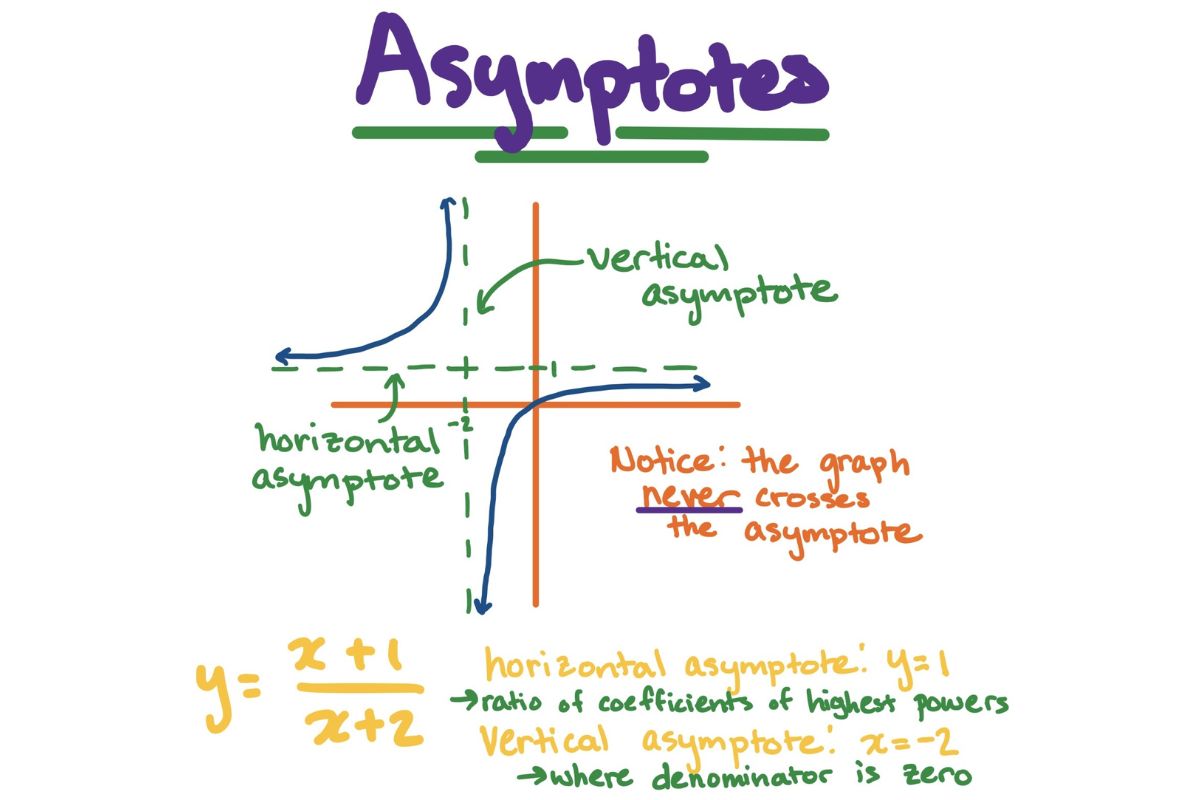
What are asymptotes? Asymptotes are lines that a curve approaches but never actually touches. Imagine a roller coaster that gets closer and closer to a track but never quite reaches it. These lines can be horizontal, vertical, or even slanted. They play a crucial role in understanding the behavior of graphs, especially in calculus. For instance, the graph of the function ( y = \frac{1}{x} ) has both a vertical and a horizontal asymptote. Knowing about asymptotes helps in predicting how functions behave at extreme values. Ready to dive into 29 intriguing facts about these mathematical wonders? Let's get started!
What is an Asymptote?
An asymptote is a line that a curve approaches but never actually touches. These lines can be horizontal, vertical, or even slanted. They play a crucial role in understanding the behavior of functions, especially in calculus and algebra.
- The term "asymptote" comes from the Greek word "asymptotos," meaning "not falling together."
- Asymptotes are used to describe the behavior of functions as they approach infinity or a specific point.
- Horizontal asymptotes occur when the value of a function approaches a constant as the input grows larger or smaller.
- Vertical asymptotes happen when the function's value increases or decreases without bound as the input approaches a specific value.
- Slant (or oblique) asymptotes occur when the function approaches a line that isn't horizontal or vertical.
Types of Asymptotes
Different types of asymptotes help us understand various aspects of a function's behavior. Let's explore these types in more detail.
- Horizontal asymptotes are often found in rational functions where the degree of the numerator is less than or equal to the degree of the denominator.
- Vertical asymptotes typically occur in rational functions where the denominator equals zero.
- Slant asymptotes appear when the degree of the numerator is exactly one more than the degree of the denominator.
- Some functions can have more than one type of asymptote.
- Trigonometric functions like tangent and cotangent have vertical asymptotes at specific intervals.
Real-World Applications
Asymptotes aren't just abstract mathematical concepts; they have practical applications in various fields.
- In physics, asymptotes can describe the behavior of waves and oscillations.
- Economics uses asymptotes to model supply and demand curves.
- Engineering often involves asymptotic analysis to understand system behavior under extreme conditions.
- In biology, asymptotes can model population growth and decay.
- Asymptotes help in computer science for analyzing algorithms' time complexity.
Graphing Asymptotes
Graphing asymptotes helps visualize how functions behave near these lines. Here's what you need to know.
- To find horizontal asymptotes, examine the limits of the function as the input approaches infinity.
- Vertical asymptotes can be found by setting the denominator of a rational function to zero and solving for the input.
- Slant asymptotes require polynomial long division to determine the linear equation the function approaches.
- Graphing calculators and software can automatically identify and plot asymptotes.
- Understanding asymptotes helps in sketching accurate graphs of complex functions.
Asymptotes in Calculus
Calculus provides tools to analyze asymptotes more rigorously. Let's see how.
- Limits are used to define asymptotes formally.
- Derivatives can help identify the slope of slant asymptotes.
- Integrals involving asymptotic functions often require special techniques like improper integrals.
- Asymptotic behavior is crucial in understanding infinite series and sequences.
- Calculus students often encounter asymptotes in problems involving rational functions and limits.
Fun Facts about Asymptotes
Asymptotes have some interesting and quirky aspects that make them fascinating.
- The concept of asymptotes dates back to ancient Greek mathematicians like Apollonius.
- Asymptotes can be found in art, particularly in perspective drawing techniques.
- Some fractals exhibit asymptotic behavior, creating intricate and beautiful patterns.
- Asymptotes can be used in game design to create challenging levels that seem impossible to beat but are just within reach.
The Final Stretch
Asymptotes might seem tricky at first, but they’re just lines that graphs get close to but never touch. They help us understand the behavior of functions, especially when values get really big or really small. Vertical asymptotes show where functions blow up, while horizontal and oblique ones tell us about end behavior. Knowing about asymptotes can make graphing functions easier and give insight into limits and continuity.
Remember, asymptotes aren’t just for math class. They pop up in real life too, like in physics and economics. So next time you see a graph, look for those lines that the curve gets close to. They’re like secret guides showing you what’s happening behind the scenes. Keep practicing, and soon enough, asymptotes will be just another tool in your math toolkit. Happy graphing!
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
