26 Facts About Circumcenter

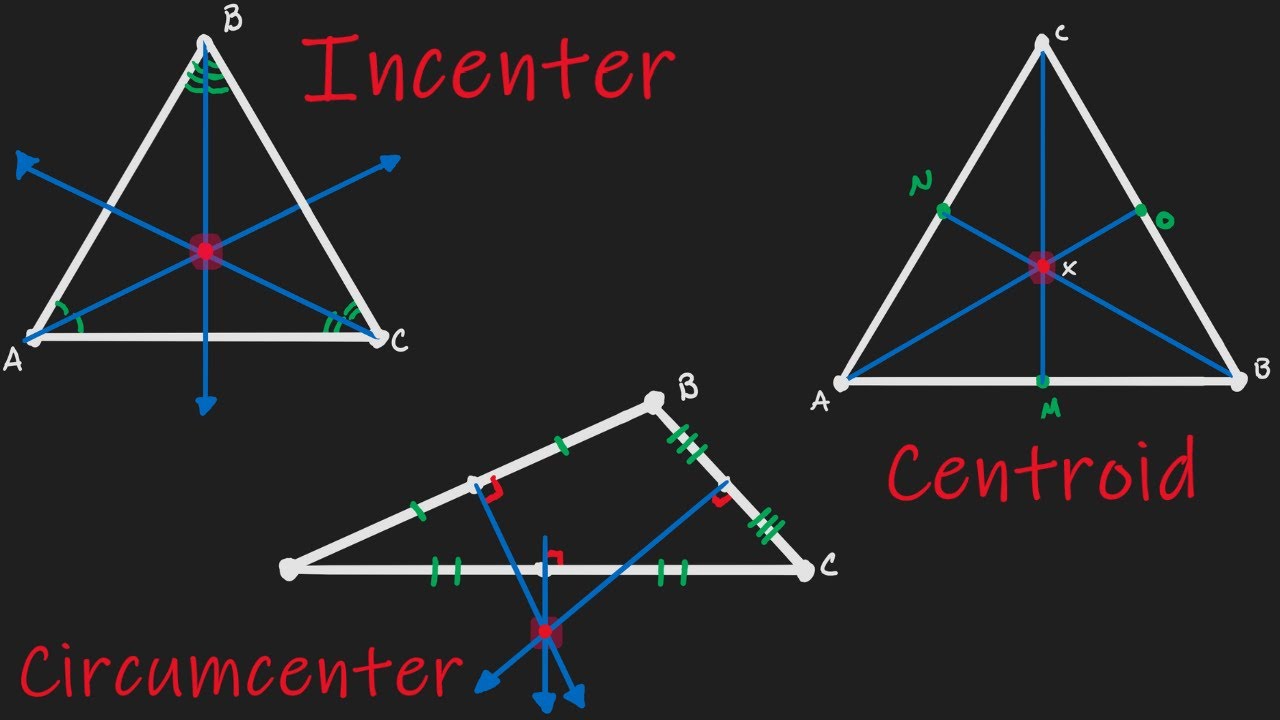
What is a Circumcenter?

The circumcenter is a fascinating concept in geometry. It's the point where the perpendicular bisectors of a triangle intersect. This unique point has several intriguing properties and applications.

1. 01

   The circumcenter is equidistant from all three vertices of the triangle. This means if you draw a circle with the circumcenter as the center, it will pass through all three vertices.

2. 02

   The circumcenter can be inside, outside, or on the triangle. For acute triangles, it's inside. For obtuse triangles, it's outside. For right triangles, it's on the hypotenuse.

3. 03

   The circle that passes through all three vertices of a triangle is called the circumcircle. The circumcenter is the center of this circle.

4. 04

   The circumcenter is one of the triangle's four main centers. The others are the centroid, orthocenter, and incenter.

5. 05

   In a right triangle, the circumcenter is the midpoint of the hypotenuse. This is because the hypotenuse is the diameter of the circumcircle.

How to Find the Circumcenter?

Finding the circumcenter involves some straightforward steps. Here's how you can locate this point in any triangle.

6. 06

   First, find the midpoint of each side of the triangle. These midpoints are crucial for the next step.

7. 07

   Draw a perpendicular line from each midpoint to the opposite side. These lines are called perpendicular bisectors.

8. 08

   The point where all three perpendicular bisectors intersect is the circumcenter. This point is equidistant from all three vertices of the triangle.

9. 09

   You can use coordinate geometry to find the circumcenter's coordinates. This involves solving equations of the perpendicular bisectors.

10. 10

    In an equilateral triangle, the circumcenter is the same as the centroid and incenter. This is because all sides and angles are equal.

Properties of the Circumcenter

The circumcenter has several unique properties that make it a vital concept in geometry.

11. 11

    The circumcenter is the only point that is equidistant from all three vertices of a triangle. This property is used in various geometric constructions.

12. 12

    The circumcenter's location depends on the type of triangle. For example, in an obtuse triangle, it's outside the triangle.

13. 13

    The circumcenter can be used to construct the circumcircle, which is essential in many geometric proofs and problems.

14. 14

    The circumcenter is the center of the circle that circumscribes the triangle. This circle is called the circumcircle.

15. 15

    The radius of the circumcircle is called the circumradius. It is the distance from the circumcenter to any of the triangle's vertices.

Applications of the Circumcenter

The circumcenter isn't just a theoretical concept. It has practical applications in various fields.

16. 16

    In navigation, the circumcenter can help determine the position of a ship or aircraft relative to three known points.

17. 17

    In engineering, the circumcenter is used in the design of triangular components and structures.

18. 18

    In computer graphics, the circumcenter helps in rendering circles and arcs that pass through three points.

19. 19

    The circumcenter is used in triangulation, a method for determining distances and positions in surveying and mapping.

20. 20

    In robotics, the circumcenter helps in path planning and obstacle avoidance.

Fun Facts about the Circumcenter

Here are some interesting tidbits about the circumcenter that you might not know.

21. 21

    The concept of the circumcenter dates back to ancient Greek mathematicians like Euclid and Archimedes.

22. 22

    The circumcenter is one of the nine-point circle's points, a circle that passes through nine significant points of a triangle.

23. 23

    The circumcenter can be used to find the Euler line, a line that passes through several important points of a triangle, including the centroid, orthocenter, and circumcenter.

24. 24

    In a scalene triangle, the circumcenter is unique and doesn't coincide with any other triangle center.

25. 25

    The circumcenter's properties are used in various mathematical proofs and theorems, making it a fundamental concept in geometry.

26. 26

    The circumcenter can be visualized using dynamic geometry software, which helps in understanding its properties and applications better.

The Heart of Triangles

Understanding the circumcenter of a triangle opens up a world of geometric wonders. This unique point, equidistant from all three vertices, plays a crucial role in various mathematical applications. From engineering to astronomy, the circumcenter's properties are utilized in numerous fields.

Knowing how to locate the circumcenter can simplify complex problems and enhance your problem-solving skills. Whether you're a student, teacher, or just a math enthusiast, grasping this concept can be incredibly rewarding.

Triangles, with their circumcenters, remind us of the beauty and precision in mathematics. They show how even the simplest shapes can hold profound secrets. So next time you see a triangle, think about its circumcenter and the fascinating geometry behind it. Happy learning!