10 Facts You Must Know About Seifert-van Kampen Theorem

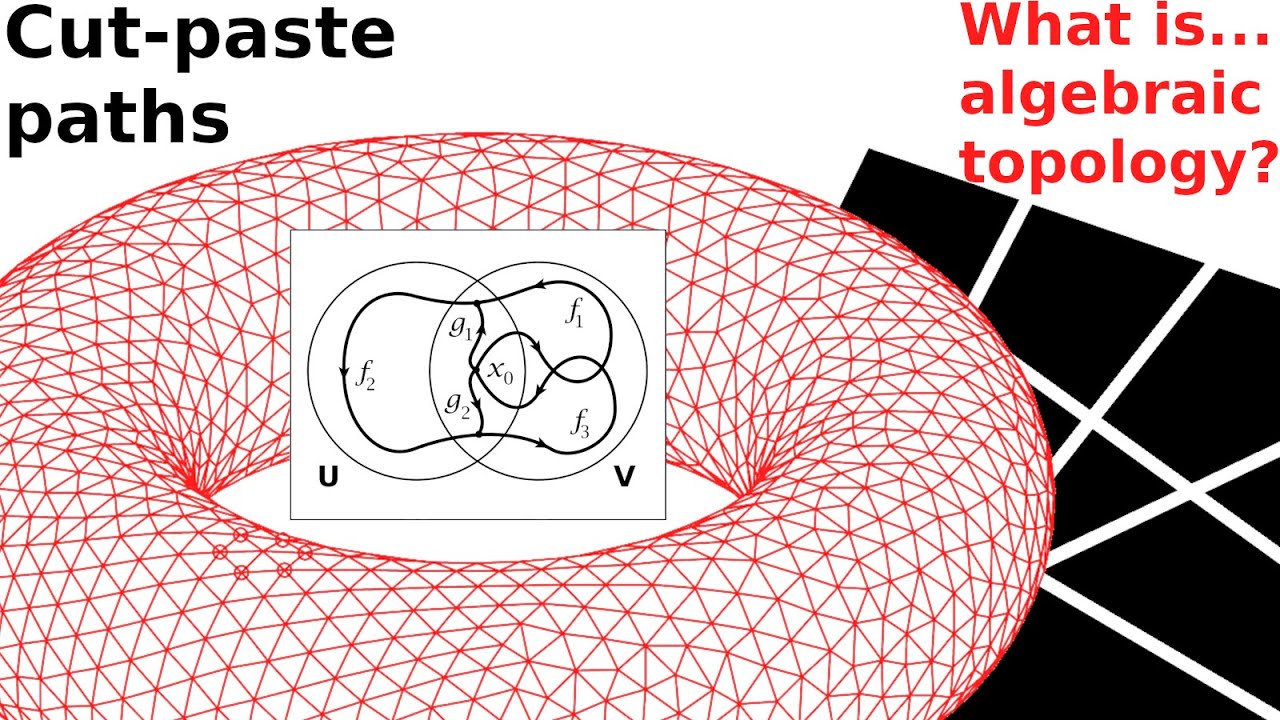
The Seifert-van Kampen Theorem is a Fundamental Result in Algebraic Topology

The Seifert-van Kampen Theorem is a fundamental result in algebraic topology that provides a powerful tool for understanding the fundamental group of a space. This theorem is essential for studying the connectivity and shape of spaces, making it a cornerstone of modern mathematics.

It Allows for the Computation of the Fundamental Group of a Space

One of the key facts about the Seifert-van Kampen Theorem is that it allows mathematicians to compute the fundamental group of a space by decomposing the space into simpler, more manageable pieces. This decomposition technique is invaluable for analyzing the fundamental group of complex spaces, enabling mathematicians to gain deep insights into the topological properties of various structures.

The Theorem Takes into Account the Interactions Between Different Parts of a Space

Another crucial aspect of the Seifert-van Kampen Theorem is its consideration of the interactions between different parts of a space. By accounting for how these components connect and overlap, the theorem provides a comprehensive framework for understanding the fundamental group in a holistic manner.

It Plays a Vital Role in Understanding the Topological Structure of Spaces

The Seifert-van Kampen Theorem plays a vital role in understanding the topological structure of spaces, shedding light on the intricate relationships between different regions within a space. This deepens our comprehension of the underlying geometry and connectivity, offering profound insights into the nature of spaces.

The Theorem Has Far-Reaching Applications in Various Mathematical Fields

Beyond its foundational significance in algebraic topology, the Seifert-van Kampen Theorem has far-reaching applications in diverse mathematical fields. Its utility extends to areas such as differential geometry, geometric group theory, and manifold theory, making it a versatile and indispensable tool for mathematicians across different disciplines.

It Empowers Mathematicians to Tackle Complex Topological Problems

The Seifert-van Kampen Theorem empowers mathematicians to tackle complex topological problems by providing a systematic approach to analyzing the fundamental group of spaces. This capability to address intricate challenges in topology underscores the theorem's profound impact on the advancement of mathematical research.

The Theorem Is Named After Its Pioneering Mathematicians

The Seifert-van Kampen Theorem is named after the pioneering mathematicians Herbert Seifert and Egbert van Kampen, who made significant contributions to the development of algebraic topology. Their groundbreaking work laid the foundation for this theorem, cementing their legacy in the annals of mathematical history.

It Illuminates the Intrinsic Connectivity of Geometric Structures

An illuminating aspect of the Seifert-van Kampen Theorem is its ability to unveil the intrinsic connectivity of geometric structures, unraveling the underlying relationships and linkages within complex spaces. This illumination enriches our understanding of the geometric fabric that underpins diverse mathematical constructs.

The Theorem Facilitates the Analysis of Homotopy Equivalences

In the realm of homotopy theory, the Seifert-van Kampen Theorem facilitates the analysis of homotopy equivalences between spaces, offering a powerful framework for comparing their topological properties. This capability to discern homotopical similarities contributes to the broader comprehension of spaces and their topological transformations.

It Continues to Inspire New Discoveries and Theoretical Breakthroughs

The enduring legacy of the Seifert-van Kampen Theorem lies in its capacity to inspire new discoveries and theoretical breakthroughs in the realm of algebraic topology. Its profound implications continue to shape the landscape of modern mathematics, fueling ongoing exploration and innovation in the field.

The Seifert-van Kampen Theorem stands as a testament to the profound interplay between algebraic topology and geometric analysis, offering a rich tapestry of insights into the fundamental group of spaces and their topological intricacies. As mathematicians delve deeper into the applications and implications of this theorem, its enduring relevance and impact on mathematical research continue to unfold, shaping the trajectory of algebraic topology and its interconnected disciplines.

Conclusion

In conclusion, the Seifert-van Kampen Theorem is a powerful tool in algebraic topology, providing a means to understand the fundamental group of a space in terms of its subspaces. This theorem has far-reaching implications in various fields, including physics, computer science, and engineering. By grasping the fundamental concepts and applications of the Seifert-van Kampen Theorem, mathematicians and researchers can unlock new insights into the topological properties of spaces and their fundamental groups.

FAQs

What is the significance of the Seifert-van Kampen Theorem?
The Seifert-van Kampen Theorem plays a crucial role in algebraic topology by enabling the computation of the fundamental group of a space based on its subspaces. This is essential for understanding the topological properties of spaces and their connectivity.

How is the Seifert-van Kampen Theorem applied in real-world scenarios?
The theorem has applications in diverse fields, such as physics, computer science, and engineering. For instance, it can be used to analyze the connectivity of networks, study the behavior of physical systems, and solve engineering problems related to space and connectivity.