40 Facts About Vector Methods

What Are Vector Methods?

Vector methods are mathematical techniques used to analyze and solve problems involving vectors. Vectors are quantities that have both magnitude and direction, making them essential in fields like physics, engineering, and computer science. Here are some fascinating facts about vector methods.

1. Vectors in Physics: Vectors are crucial in physics for representing quantities like force, velocity, and acceleration. They help in understanding the direction and magnitude of these quantities.

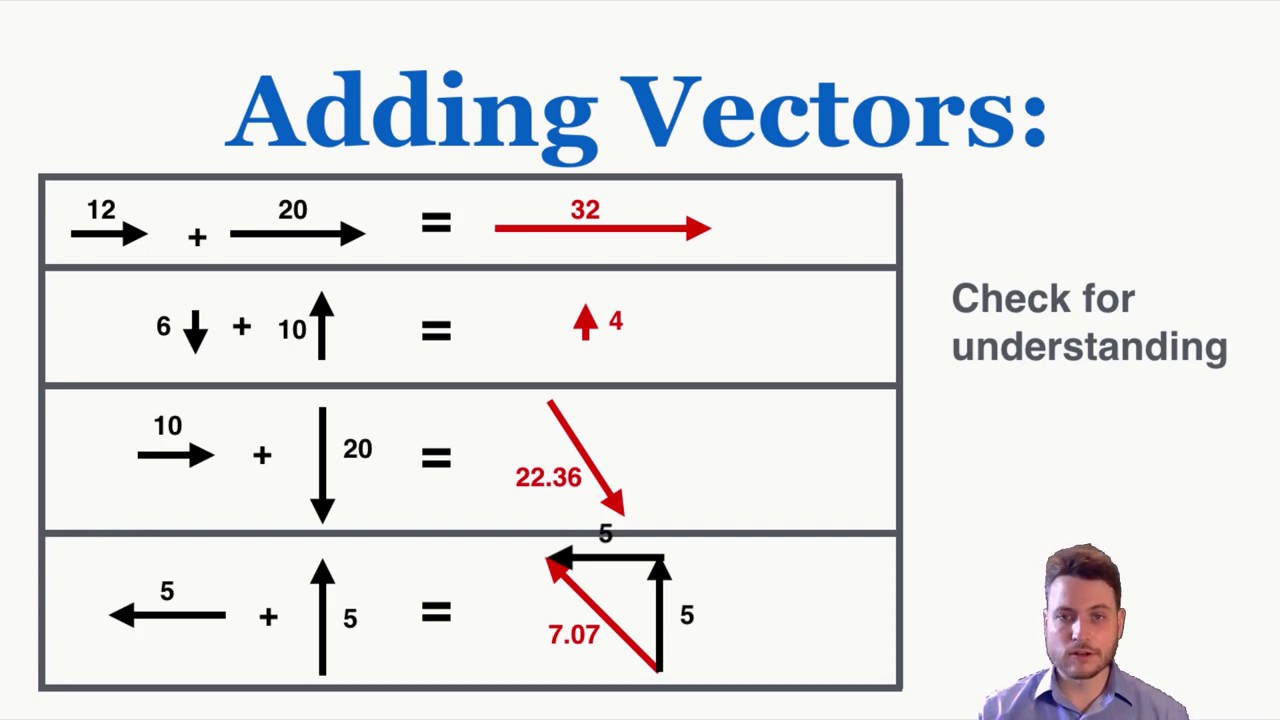
2. Vector Addition: Adding vectors involves placing them head to tail and drawing a new vector from the start of the first to the end of the last. This new vector is called the resultant.

3. Scalar Multiplication: Multiplying a vector by a scalar changes its magnitude but not its direction. This is useful in scaling vectors up or down.

4. Dot Product: The dot product of two vectors results in a scalar. It’s calculated by multiplying corresponding components and summing them up. This product is used to find the angle between vectors.

5. Cross Product: The cross product of two vectors results in another vector perpendicular to the plane of the original vectors. This is essential in finding torque and rotational forces.

6. Unit Vectors: Unit vectors have a magnitude of one and are used to indicate direction. They are fundamental in breaking down vectors into components.

7. Vector Components: Any vector can be broken down into components along the x, y, and z axes. This simplifies calculations in three-dimensional space.

8. Vector Spaces: A vector space is a collection of vectors that can be added together and multiplied by scalars. This concept is foundational in linear algebra.

9. Basis Vectors: Basis vectors are a set of vectors that, through linear combinations, can represent any vector in a given space. They provide a framework for vector spaces.

10. Orthogonal Vectors: Two vectors are orthogonal if their dot product is zero. This means they are perpendicular to each other.

Applications of Vector Methods

Vector methods are not just theoretical; they have practical applications in various fields. Here are some examples of how vectors are used in real-world scenarios.

11. Computer Graphics: Vectors are used to represent images, animations, and transformations in computer graphics. They help in rendering 3D models and simulations.

12. Navigation Systems: GPS and other navigation systems use vectors to calculate distances and directions between points on Earth.

13. Robotics: Robots use vectors to determine movement and orientation. Vectors help in programming robotic arms and navigation.

14. Engineering: Engineers use vectors to analyze forces, stresses, and strains in structures. This helps in designing safe and efficient buildings and machines.

15. Aerospace: Vectors are used to calculate trajectories, velocities, and forces acting on aircraft and spacecraft.

16. Economics: In economics, vectors represent quantities like supply and demand, helping in the analysis of market trends.

17. Machine Learning: Vectors are used to represent data points in machine learning algorithms. They help in clustering, classification, and regression tasks.

18. Physics Simulations: Vectors are essential in simulating physical phenomena like fluid dynamics, electromagnetism, and mechanics.

19. Geology: Geologists use vectors to represent the orientation of rock layers and fault lines. This helps in understanding geological formations.

20. Meteorology: Weather models use vectors to represent wind speed and direction, aiding in accurate weather forecasting.

Advanced Vector Methods

As you delve deeper into vector methods, you'll encounter more advanced techniques that offer powerful tools for analysis and problem-solving.

21. Eigenvectors and Eigenvalues: These are used in linear transformations to understand how vectors change under certain operations. They have applications in stability analysis and quantum mechanics.

22. Vector Calculus: This branch of mathematics deals with differentiation and integration of vector fields. It’s crucial in electromagnetism and fluid dynamics.

23. Gradient Vectors: The gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar. It’s used in optimization problems.

24. Divergence and Curl: These operators measure the magnitude of a vector field’s source or sink (divergence) and its rotation (curl). They are fundamental in electromagnetism and fluid dynamics.

25. Fourier Transform: This method transforms a function into its constituent frequencies. It’s used in signal processing and image analysis.

26. Laplace Transform: This technique transforms a function of time into a function of complex frequency. It’s used in control theory and differential equations.

27. Tensor Calculus: Tensors generalize vectors and matrices to higher dimensions. They are used in general relativity and continuum mechanics.

28. Vector Projections: Projecting one vector onto another helps in finding components in specific directions. This is useful in physics and engineering.

29. Vector Norms: The norm of a vector is a measure of its length or magnitude. Different norms are used in various applications, such as L1 and L2 norms in machine learning.

30. Vector Fields: A vector field assigns a vector to every point in space. They are used to represent force fields, velocity fields, and electromagnetic fields.

Fun Facts About Vectors

Vectors can be fun too! Here are some interesting and lesser-known facts about vectors.

31. Vectors in Video Games: Game developers use vectors to create realistic movements and physics in video games.

32. Vectors in Art: Artists use vectors to create scalable graphics that don’t lose quality when resized. This is common in digital art and design.

33. Vectors in Music: Audio engineers use vectors to represent sound waves and manipulate audio signals.

34. Vectors in Sports: Coaches use vectors to analyze player movements and strategies in sports like soccer and basketball.

35. Vectors in Nature: Animals like birds and fish use vectors to navigate and migrate over long distances.

36. Vectors in Medicine: Medical imaging techniques like MRI and CT scans use vectors to create detailed images of the human body.

37. Vectors in Cryptography: Cryptographers use vectors to encode and decode information securely.

38. Vectors in Astronomy: Astronomers use vectors to calculate the positions and movements of celestial bodies.

39. Vectors in Fashion: Fashion designers use vectors to create patterns and designs for clothing.

40. Vectors in Education: Teachers use vectors to explain complex concepts in subjects like physics and mathematics.

Final Thoughts on Vector Methods

Vector methods are essential tools in mathematics, physics, and engineering. They simplify complex problems, making calculations more manageable. From representing physical quantities like force and velocity to solving systems of linear equations, vectors are everywhere. Understanding vector addition, subtraction, and scalar multiplication can help in various fields, including computer graphics and machine learning.

Vectors also play a crucial role in navigation and robotics, guiding movements and optimizing paths. Their applications extend to economics, where they model and solve optimization problems. Mastering vector methods can open doors to numerous career opportunities and enhance problem-solving skills.

Whether you're a student, professional, or just curious, grasping vector methods can provide a solid foundation for tackling real-world challenges. So, keep exploring and practicing these concepts to unlock their full potential. Happy learning!