39 Facts About Geometric Algebra

What is Geometric Algebra?

Geometric Algebra (GA) is a mathematical framework that extends traditional algebra to include geometric transformations. It provides a unified language for various branches of mathematics and physics. Here are some fascinating facts about this powerful tool.

1. Geometric Algebra was developed by William Kingdon Clifford in the 19th century. He combined the ideas of algebra and geometry to create a more comprehensive mathematical system.

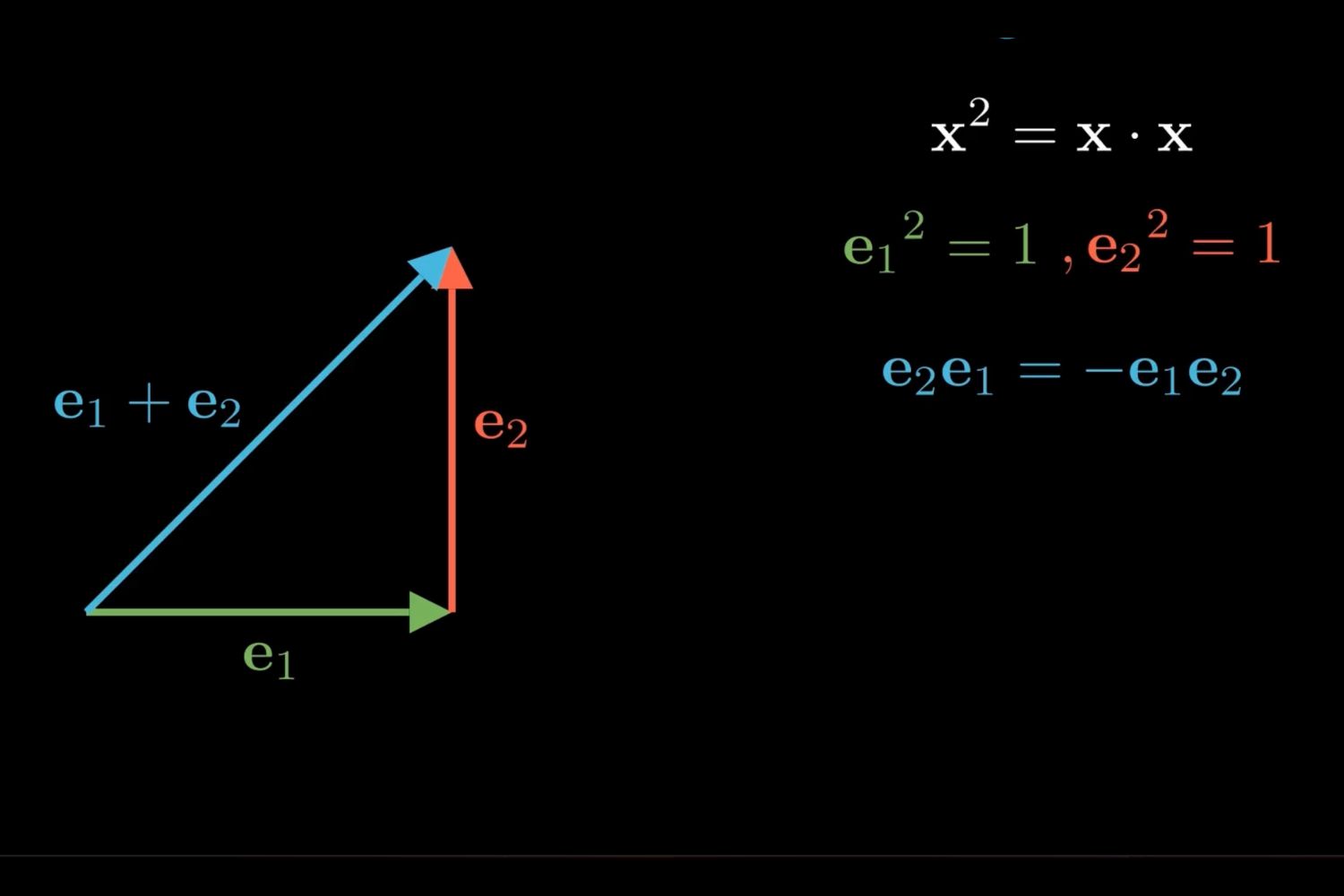
2. It generalizes complex numbers and quaternions. GA can represent complex numbers and quaternions, making it a versatile tool for various applications.

3. GA uses multivectors. Unlike traditional algebra, which uses scalars and vectors, GA employs multivectors to represent different geometric entities.

4. It simplifies the representation of rotations. In GA, rotations can be represented more compactly and intuitively than in traditional vector algebra.

Applications in Physics

Geometric Algebra has numerous applications in physics, from classical mechanics to quantum mechanics. Its ability to unify different mathematical concepts makes it invaluable.

5. GA is used in classical mechanics. It provides a more intuitive way to describe the motion of objects and the forces acting on them.

6. It plays a role in electromagnetism. GA can simplify Maxwell's equations, making them easier to understand and solve.

7. Quantum mechanics benefits from GA. It offers a new perspective on the mathematical formulation of quantum theories.

8. Relativity theory uses GA. GA helps in describing spacetime and the behavior of objects at relativistic speeds.

Benefits in Computer Science

Geometric Algebra is not just for physicists and mathematicians; it has practical applications in computer science as well.

9. GA aids in computer graphics. It simplifies the mathematics behind rendering 3D objects and animations.

10. Robotics uses GA. It helps in the precise control and movement of robotic arms and other mechanisms.

11. Machine learning benefits from GA. GA can improve the efficiency and accuracy of certain algorithms.

12. GA is used in computer vision. It helps in the recognition and interpretation of visual data.

Educational Value

Learning Geometric Algebra can provide students with a deeper understanding of both algebra and geometry, enhancing their overall mathematical skills.

13. GA bridges the gap between algebra and geometry. It provides a unified framework that makes it easier to understand both subjects.

14. It enhances problem-solving skills. GA encourages a more intuitive approach to solving complex mathematical problems.

15. GA is increasingly being included in curricula. More educational institutions are recognizing its value and incorporating it into their programs.

Historical Context

Understanding the history of Geometric Algebra can provide insights into its development and significance.

16. GA has roots in ancient Greece. The ideas behind GA can be traced back to the geometric work of Euclid and others.

17. It was influenced by Grassmann's work. Hermann Grassmann's work on linear algebra laid the groundwork for Clifford's development of GA.

18. GA was initially overlooked. For many years, GA was not widely recognized or used, but its importance has grown over time.

19. Revival in the 20th century. The work of mathematicians like David Hestenes helped revive interest in GA.

Mathematical Foundations

The mathematical principles underlying Geometric Algebra are both fascinating and complex.

20. GA extends linear algebra. It builds on the concepts of linear algebra, adding new dimensions and capabilities.

21. It includes the concept of a geometric product. This product combines the dot product and the wedge product, providing a more comprehensive operation.

22. GA uses blades. Blades are the building blocks of multivectors, representing different geometric entities.

23. It incorporates the concept of duality. Duality in GA allows for the representation of geometric entities in different forms.

Real-World Applications

Geometric Algebra is not just theoretical; it has practical applications in various fields.

24. GA is used in engineering. It helps in the design and analysis of mechanical systems.

25. It aids in navigation. GA can improve the accuracy of navigation systems, both on Earth and in space.

26. GA is used in signal processing. It helps in the analysis and manipulation of signals.

27. It has applications in computer-aided design (CAD). GA simplifies the mathematics behind CAD software.

Future Prospects

The future of Geometric Algebra looks promising, with potential applications in new and emerging fields.

28. GA could revolutionize artificial intelligence. Its ability to simplify complex mathematical operations could make AI more efficient.

29. It may play a role in quantum computing. GA could provide new ways to represent and manipulate quantum information.

30. GA could enhance virtual reality. It could improve the realism and accuracy of VR simulations.

31. It might aid in the development of new materials. GA could help in the design and analysis of advanced materials.

Challenges and Limitations

Despite its many advantages, Geometric Algebra also has some challenges and limitations.

32. GA can be difficult to learn. Its concepts are more complex than those of traditional algebra, requiring a deeper understanding of mathematics.

33. It is not yet widely adopted. While its use is growing, GA is not yet as widely used as other mathematical frameworks.

34. GA requires specialized software. Working with GA often requires specialized software, which can be a barrier to entry.

35. It can be computationally intensive. Some operations in GA can be more computationally demanding than their traditional counterparts.

Interesting Tidbits

Here are some more intriguing facts about Geometric Algebra that you might find interesting.

36. GA can describe higher-dimensional spaces. It is not limited to three dimensions, making it useful for advanced mathematical and physical theories.

37. It has connections to string theory. Some researchers believe GA could provide new insights into string theory and other advanced physical theories.

38. GA is used in cryptography. It can help in the design of more secure cryptographic systems.

39. It has artistic applications. Some artists use GA to create intricate and beautiful geometric designs.

The Final Word on Geometric Algebra

Geometric Algebra isn't just for math geeks. It's a powerful tool that simplifies complex problems in physics, engineering, and computer science. From understanding rotations to solving linear equations, this branch of mathematics offers practical solutions. It bridges the gap between algebra and geometry, making it easier to visualize and solve problems.

Whether you're a student, a professional, or just curious, diving into Geometric Algebra can open up new ways of thinking. It’s not just about numbers and equations; it’s about seeing the world in a different light. So, next time you encounter a tricky problem, remember that Geometric Algebra might just have the answer.

Keep exploring, keep questioning, and let the power of Geometric Algebra guide you through the complexities of the mathematical world.