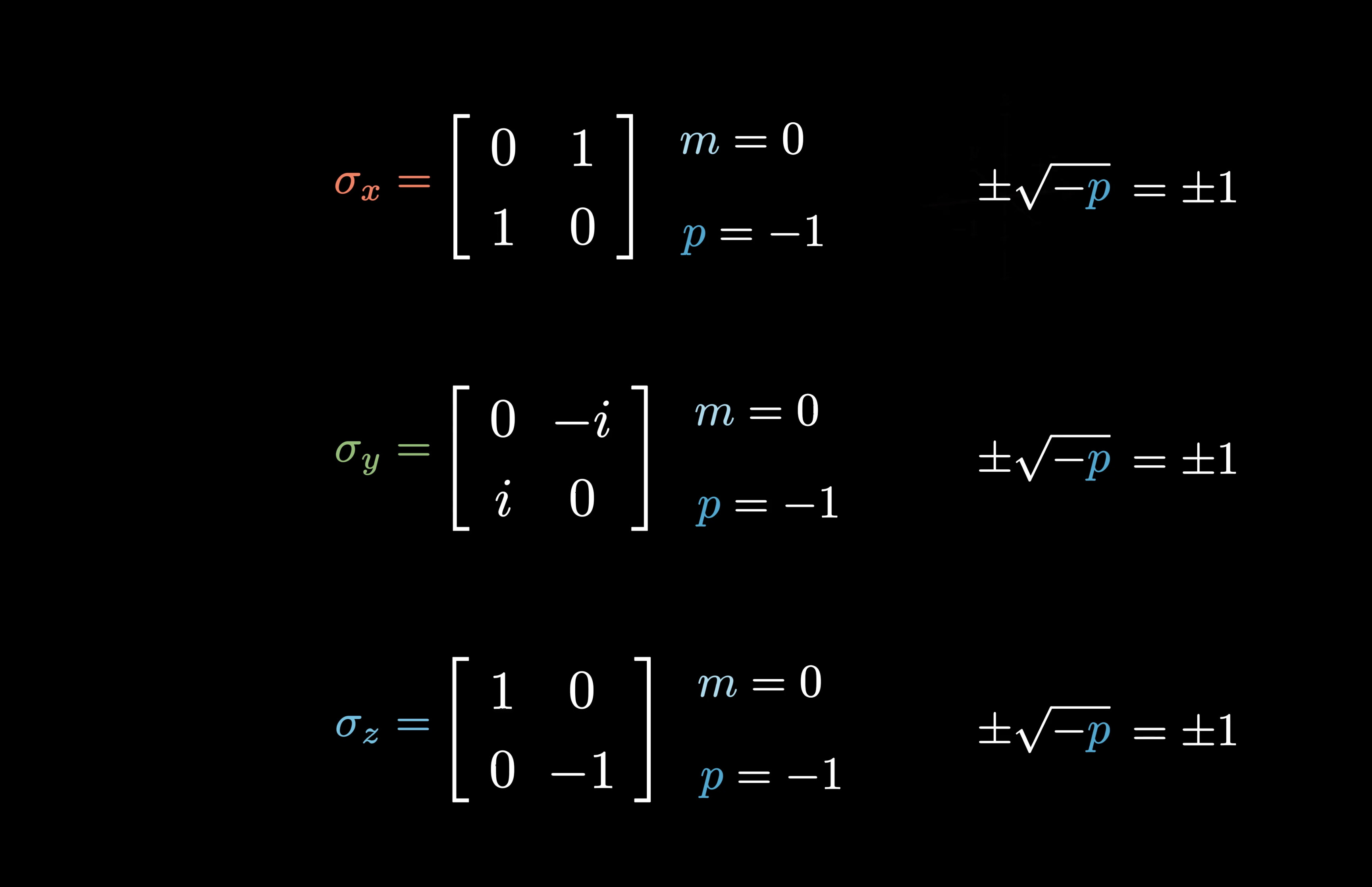
Eigenvalues might sound like a complex math term, but they play a huge role in many areas of science and engineering. Ever wondered how Google ranks web pages or how your phone recognizes your face? Eigenvalues are behind these technologies! They help in simplifying complex problems, making them easier to solve. From quantum mechanics to machine learning, they are everywhere. Understanding eigenvalues can open up a world of possibilities, whether you're a student, a professional, or just curious. Ready to dive into some fascinating facts about eigenvalues? Let's get started!
What Are Eigenvalues?
Eigenvalues are a fundamental concept in linear algebra. They help us understand the behavior of linear transformations and matrices. Here are some fascinating facts about eigenvalues:
-
Definition: An eigenvalue is a scalar that, when multiplied by a given vector (called an eigenvector), does not change the direction of that vector.
-
Origin: The term "eigenvalue" comes from the German word "eigen," meaning "own" or "characteristic."
-
Applications: Eigenvalues are used in various fields, including physics, engineering, computer science, and economics.
-
Matrix Representation: For a square matrix (A), an eigenvalue (lambda) satisfies the equation (Amathbf{v} = lambdamathbf{v}), where (mathbf{v}) is the eigenvector.
-
Characteristic Polynomial: The eigenvalues of a matrix are the roots of its characteristic polynomial, which is derived from the determinant of (A – lambda I).
Eigenvalues in Real-World Applications
Eigenvalues aren't just theoretical; they have practical uses in many real-world scenarios. Let's explore some of these applications:
-
Google PageRank: Google uses eigenvalues to rank web pages in its search engine results.
-
Quantum Mechanics: In quantum mechanics, eigenvalues represent possible measurement outcomes of an observable.
-
Stability Analysis: Engineers use eigenvalues to analyze the stability of structures and systems.
-
Principal Component Analysis (PCA): PCA, a technique in statistics, uses eigenvalues to reduce the dimensionality of data.
-
Vibration Analysis: Eigenvalues help determine the natural frequencies of vibrating systems, such as bridges and buildings.
Mathematical Properties of Eigenvalues
Eigenvalues have several interesting mathematical properties. Here are some key ones:
-
Sum of Eigenvalues: The sum of the eigenvalues of a matrix equals the trace of the matrix (the sum of its diagonal elements).
-
Product of Eigenvalues: The product of the eigenvalues of a matrix equals the determinant of the matrix.
-
Eigenvalues of Diagonal Matrices: For a diagonal matrix, the eigenvalues are simply the diagonal elements.
-
Eigenvalues of Triangular Matrices: For upper or lower triangular matrices, the eigenvalues are the diagonal elements.
-
Multiplicity: Eigenvalues can have algebraic multiplicity (number of times they appear as roots of the characteristic polynomial) and geometric multiplicity (number of linearly independent eigenvectors associated with them).
Eigenvalues in Different Types of Matrices
Different types of matrices have unique eigenvalue properties. Let's look at some examples:
-
Symmetric Matrices: Eigenvalues of symmetric matrices are always real numbers.
-
Hermitian Matrices: Eigenvalues of Hermitian matrices (complex analogs of symmetric matrices) are also real.
-
Orthogonal Matrices: Eigenvalues of orthogonal matrices have an absolute value of 1.
-
Unitary Matrices: Eigenvalues of unitary matrices lie on the complex unit circle.
-
Positive Definite Matrices: Eigenvalues of positive definite matrices are all positive.
Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are closely related. Here are some facts about their relationship:
-
Normalization: Eigenvectors can be normalized to have a unit length.
-
Orthogonality: Eigenvectors of symmetric matrices corresponding to distinct eigenvalues are orthogonal.
-
Eigenbasis: A set of eigenvectors can form a basis for the vector space, known as an eigenbasis.
-
Diagonalization: A matrix can be diagonalized if it has a full set of linearly independent eigenvectors.
-
Spectral Theorem: The spectral theorem states that any symmetric matrix can be diagonalized by an orthogonal matrix.
Computational Aspects of Eigenvalues
Computing eigenvalues can be challenging, but several methods exist to make it easier. Here are some computational facts:
-
Power Iteration: Power iteration is a simple algorithm to find the largest eigenvalue of a matrix.
-
QR Algorithm: The QR algorithm is a more sophisticated method used to find all eigenvalues of a matrix.
-
Jacobi Method: The Jacobi method is used for finding eigenvalues of symmetric matrices.
-
Lanczos Algorithm: The Lanczos algorithm is efficient for finding a few eigenvalues of large sparse matrices.
-
Numerical Stability: Some algorithms for computing eigenvalues are more numerically stable than others, affecting their accuracy.
Historical Context of Eigenvalues
Eigenvalues have a rich history in mathematics. Here are some historical facts:
-
Discovery: Eigenvalues were first studied by mathematicians in the 18th century.
-
Contributors: Notable contributors to the theory of eigenvalues include Euler, Lagrange, and Cauchy.
-
Development: The formal theory of eigenvalues and eigenvectors was developed in the 19th century.
-
Applications: Early applications of eigenvalues were in solving differential equations and studying vibrations.
-
Modern Use: Today, eigenvalues are a standard topic in linear algebra courses and have numerous applications in science and engineering.
Fun Facts About Eigenvalues
Let's end with some fun and quirky facts about eigenvalues:
-
Eigenfaces: In facial recognition technology, "eigenfaces" are used to represent and recognize human faces.
-
Music: Eigenvalues are used in music theory to analyze and compose music.
-
Art: Some artists use eigenvalues and eigenvectors to create mathematically inspired artwork.
Final Thoughts on Eigenvalues
Eigenvalues are more than just numbers in a matrix. They play a crucial role in various fields like physics, engineering, and computer science. Understanding them can help solve complex problems, from predicting system behavior to optimizing algorithms. They’re essential in quantum mechanics, stability analysis, and even Google's search algorithms. Knowing these 38 facts can give you a solid foundation, making complex topics more approachable. Whether you're a student, a professional, or just curious, grasping eigenvalues can open doors to new insights and opportunities. So, keep exploring and applying this knowledge in your studies or work. Eigenvalues might seem daunting at first, but with practice, they become a powerful tool in your mathematical toolkit. Happy learning!
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
