Lie Groups might sound like something from a spy novel, but they’re actually a fascinating part of mathematics. Lie Groups are named after the Norwegian mathematician Sophus Lie and are used to study continuous symmetry. These groups play a crucial role in various fields, including physics, engineering, and even cryptography. Ever wondered how scientists describe the symmetry of molecules or the behavior of particles in quantum mechanics? Lie Groups are the answer! They help us understand complex systems by breaking them down into simpler, symmetrical parts. Ready to dive into the world of Lie Groups? Here are 34 intriguing facts that will make you see math in a whole new light!
What Are Lie Groups?
Lie groups are mathematical structures that combine algebra and geometry. They play a crucial role in various fields, including physics and engineering. Here are some fascinating facts about Lie groups.
-
Named After Sophus Lie
Lie groups are named after Norwegian mathematician Sophus Lie, who developed the theory in the late 19th century. -
Continuous Symmetry
They describe continuous symmetries, which means they can smoothly transform from one state to another without any abrupt changes. -
Applications in Physics
Lie groups are essential in physics, especially in the study of particle physics and quantum mechanics. -
Matrix Groups
Many Lie groups can be represented as groups of matrices, making them easier to study and apply. -
Lie Algebras
Associated with every Lie group is a Lie algebra, which helps in understanding the group's structure and properties.
Historical Background
The development of Lie groups has a rich history, influenced by many brilliant minds. Let's dive into some historical facts.
-
Sophus Lie's Contribution
Sophus Lie initially developed the concept to study differential equations and their symmetries. -
Élie Cartan's Work
French mathematician Élie Cartan made significant contributions by classifying simple Lie algebras. -
Felix Klein's Influence
Felix Klein's Erlangen Program emphasized the importance of symmetry in geometry, indirectly promoting the study of Lie groups. -
Connection to Group Theory
Lie groups are a special case of group theory, which studies sets equipped with an operation that combines any two elements to form a third element. -
20th Century Advancements
The 20th century saw significant advancements in the theory of Lie groups, particularly through the work of Hermann Weyl and others.
Types of Lie Groups
Lie groups come in various types, each with unique properties and applications. Here are some key types.
-
Compact Lie Groups
These are Lie groups that are compact as topological spaces, meaning they are closed and bounded. -
Non-Compact Lie Groups
Non-compact Lie groups are not bounded, making them more complex to study. -
Simple Lie Groups
Simple Lie groups are non-abelian and have no non-trivial normal subgroups. -
Semisimple Lie Groups
Semisimple Lie groups are built from simple Lie groups and have no abelian normal subgroups. -
Abelian Lie Groups
These are Lie groups where the group operation is commutative, meaning the order of operations does not matter.
Applications in Modern Science
Lie groups are not just theoretical constructs; they have practical applications in modern science and technology.
-
Quantum Mechanics
In quantum mechanics, Lie groups help describe the symmetries of physical systems. -
Particle Physics
The Standard Model of particle physics relies heavily on Lie groups to describe fundamental particles and their interactions. -
General Relativity
Einstein's theory of general relativity uses Lie groups to describe the symmetries of spacetime. -
Control Theory
In engineering, Lie groups are used in control theory to design systems that can maintain desired outputs. -
Robotics
Robotics uses Lie groups to model and control the movement of robots.
Mathematical Properties
Lie groups have fascinating mathematical properties that make them a rich area of study.
-
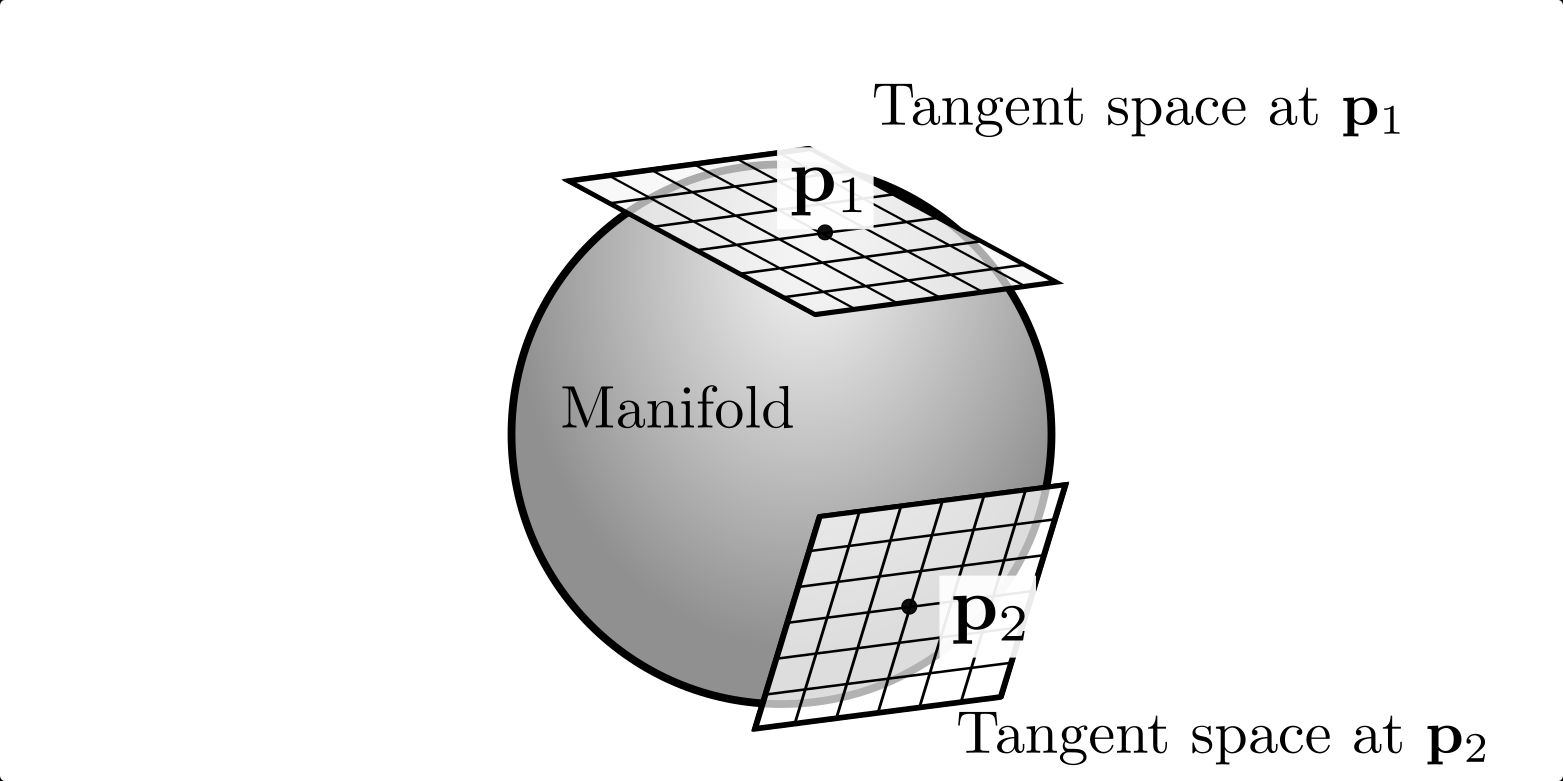
Manifold Structure
Every Lie group is also a smooth manifold, meaning it has a structure that allows for calculus to be performed. -
Exponential Map
The exponential map connects Lie algebras to Lie groups, providing a powerful tool for analysis. -
Homogeneous Spaces
Lie groups can act on homogeneous spaces, which are spaces that look the same at every point. -
Representation Theory
Representation theory studies how Lie groups can be represented by matrices, revealing deep insights into their structure. -
Invariant Measures
Lie groups have invariant measures, which remain unchanged under the group's operations.
Famous Examples
Some Lie groups are particularly famous and widely studied. Here are a few notable examples.
-
SO(3)
SO(3) is the group of rotations in three-dimensional space, crucial in physics and engineering. -
SU(2)
SU(2) is important in quantum mechanics and describes spin-1/2 particles. -
SL(2, R)
SL(2, R) consists of 2×2 real matrices with determinant 1, used in various mathematical contexts. -
U(1)
U(1) is the group of complex numbers with absolute value 1, fundamental in electromagnetism. -
E8
E8 is an exceptional Lie group with a highly complex structure, studied in theoretical physics.
Challenges in Study
Studying Lie groups presents several challenges due to their complexity and abstract nature.
-
Complex Analysis
Understanding Lie groups often requires advanced knowledge of complex analysis. -
High Dimensionality
Many Lie groups exist in high-dimensional spaces, making visualization and computation difficult. -
Abstract Concepts
The abstract nature of Lie groups can be challenging for those new to the field. -
Interdisciplinary Knowledge
Studying Lie groups often requires knowledge from multiple disciplines, including algebra, geometry, and physics.
Final Thoughts on Lie Groups
Lie groups, with their fascinating blend of algebra and geometry, play a crucial role in both mathematics and physics. They help us understand symmetries in nature, from the smallest particles to the vast cosmos. These groups are not just abstract concepts; they have practical applications in areas like quantum mechanics, relativity, and even robotics. By studying Lie groups, scientists and mathematicians can solve complex problems and make groundbreaking discoveries. So, next time you hear about symmetry in science, remember the importance of Lie groups. They’re more than just mathematical structures; they’re keys to unlocking the mysteries of our universe. Dive deeper into this topic, and you’ll find a world rich with patterns and connections that shape our understanding of reality.
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
