30 Facts About Measure Theory

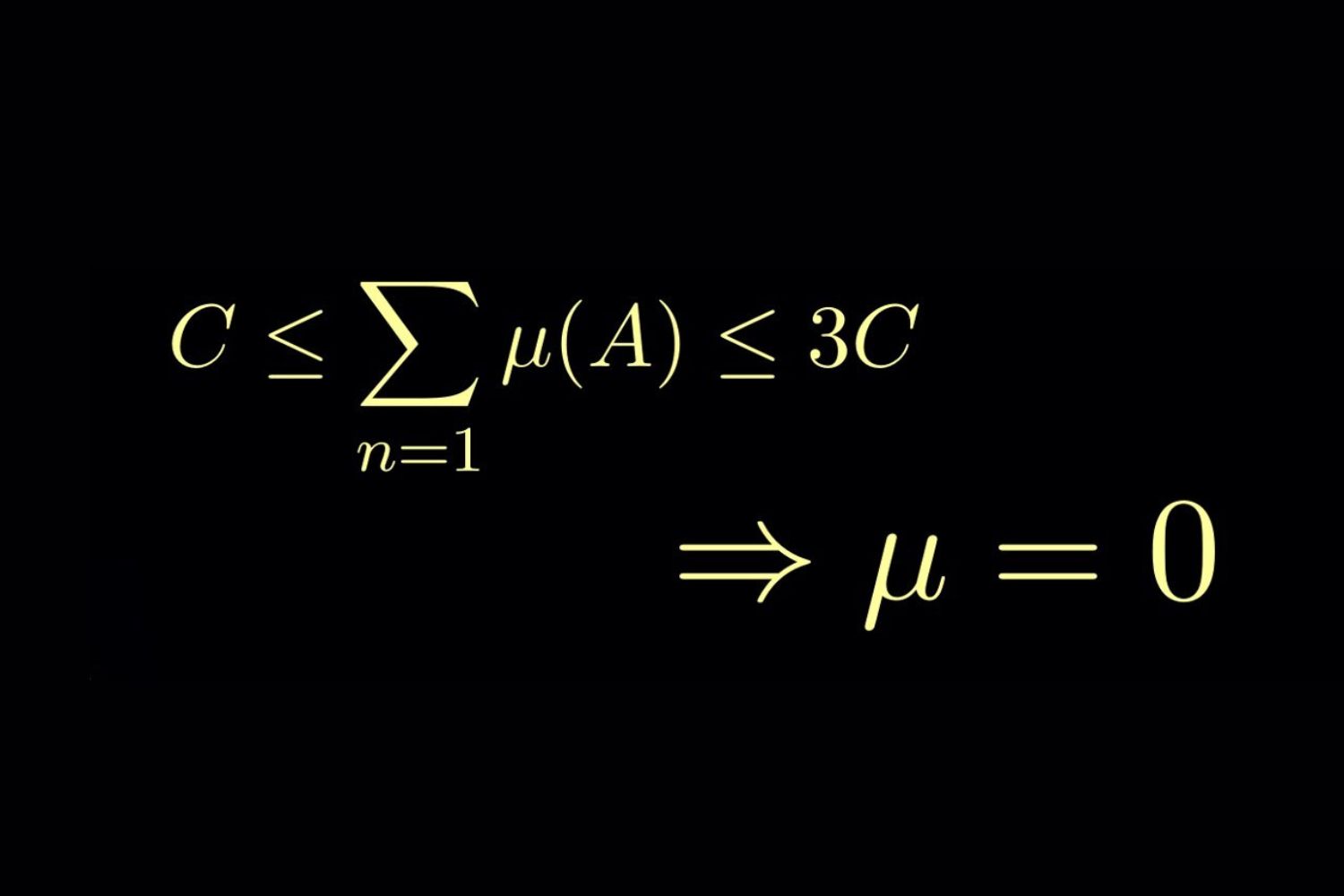
What is Measure Theory?

Measure theory is a branch of mathematics that studies ways to assign a size or measure to sets, which can be more complex than simple geometric shapes. It's crucial for understanding probability, integration, and real analysis.

1. Measure theory was developed in the early 20th century by French mathematician Henri Lebesgue.
2. It provides the foundation for modern probability theory.
3. The concept of a "measure" generalizes the idea of length, area, and volume.
4. Lebesgue's integral is a key concept in measure theory, extending the idea of integration.
5. Measure theory helps in defining and working with infinite-dimensional spaces.

Key Concepts in Measure Theory

Understanding measure theory requires grasping several fundamental concepts. These ideas form the backbone of the subject and are essential for further study.

6. A sigma-algebra is a collection of sets closed under countable unions and complements.
7. A measure is a function that assigns a non-negative number to sets in a sigma-algebra.
8. The Lebesgue measure is the most common measure on the real line, generalizing the length of intervals.
9. Measurable functions are functions compatible with the measure structure, crucial for integration.
10. The Borel sigma-algebra is generated by open sets in a topological space, important in real analysis.

Applications of Measure Theory

Measure theory isn't just theoretical; it has practical applications in various fields. These applications demonstrate its importance beyond pure mathematics.

11. Measure theory underpins modern probability theory, essential for statistics and risk assessment.
12. It's used in quantum mechanics to describe probabilities of different outcomes.
13. In economics, measure theory helps in modeling and analyzing market behaviors.
14. Measure theory is crucial for ergodic theory, studying the long-term average behavior of dynamical systems.
15. It's applied in information theory to measure the amount of information in signals.

Advanced Topics in Measure Theory

For those delving deeper, measure theory offers advanced topics that explore more complex and abstract ideas. These topics are often studied in higher-level mathematics courses.

16. Radon-Nikodym theorem provides conditions under which one measure can be derived from another.
17. Fubini's theorem allows the evaluation of double integrals as iterated integrals.
18. Carathéodory's extension theorem helps in constructing measures from pre-measures.
19. Hausdorff measure generalizes the concept of measure to fractals and other irregular sets.
20. Martingale theory uses measure theory to study sequences of random variables.

Historical Development of Measure Theory

The history of measure theory is rich with contributions from various mathematicians. Understanding its development provides context for its current form.

21. Henri Lebesgue introduced the concept of measure and the Lebesgue integral in 1902.
22. Émile Borel and Constantin Carathéodory made significant contributions to the formalization of measure theory.
23. Andrey Kolmogorov used measure theory to formalize probability theory in the 1930s.
24. Paul Halmos wrote "Measure Theory," a seminal textbook that influenced generations of mathematicians.
25. The development of measure theory was crucial for the advancement of functional analysis.

Measure Theory in Modern Mathematics

Measure theory continues to evolve and find new applications in modern mathematics. Its principles are foundational for many contemporary mathematical theories.

26. Measure theory is essential for the study of stochastic processes, which model random phenomena over time.
27. It's used in functional analysis to study spaces of functions and their properties.
28. Harmonic analysis relies on measure theory to study functions and signals.
29. Measure theory is applied in partial differential equations to understand solutions' behavior.
30. It's crucial for mathematical finance, modeling and analyzing financial markets and instruments.

Measure Theory's Impact

Measure theory isn't just for mathematicians. It plays a crucial role in probability theory, statistics, economics, and even quantum mechanics. Understanding this field can open doors to advanced studies and practical applications in various disciplines.

From Lebesgue integration to sigma-algebras, these concepts help us make sense of complex data and phenomena. Whether you're a student, researcher, or just curious, diving into measure theory can be incredibly rewarding.

Remember, the beauty of measure theory lies in its ability to provide a rigorous foundation for understanding the world around us. So, next time you encounter a complex problem, think about how measure theory might offer a solution.

Keep exploring, keep questioning, and you'll find that measure theory is more than just a set of abstract concepts—it's a powerful tool for making sense of the universe.