29 Facts About Central Limit

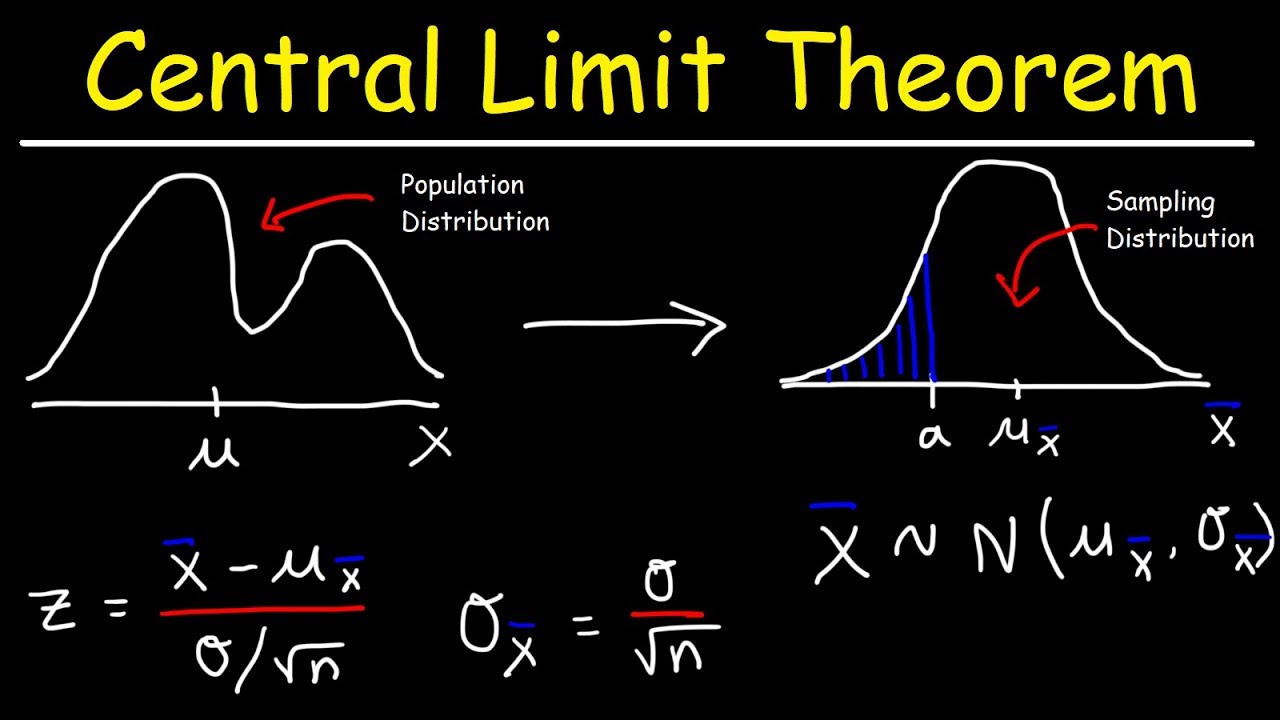
What is the Central Limit Theorem?

The Central Limit Theorem (CLT) is a fundamental concept in statistics. It explains why many distributions tend to be normal, or bell-shaped, even if the original data isn't. Here are some fascinating facts about this theorem.

1. The Central Limit Theorem states that the distribution of sample means approximates a normal distribution as the sample size becomes larger, regardless of the population's distribution.

2. The theorem applies to sums and averages of random variables, making it versatile in various statistical applications.

3. The CLT is crucial for inferential statistics, allowing statisticians to make predictions about population parameters based on sample data.

Historical Background of the Central Limit Theorem

Understanding the history of the CLT gives insight into its development and significance in statistics.

4. The concept of the CLT was first introduced by Abraham de Moivre in 1733 while studying the probabilities of gambling.

5. Pierre-Simon Laplace expanded on de Moivre's work in the early 19th century, applying the theorem to errors in astronomical observations.

6. The formal definition and proof of the CLT were provided by Russian mathematician Aleksandr Lyapunov in 1901.

Applications of the Central Limit Theorem

The CLT has numerous practical applications across different fields. Here are some examples:

7. In quality control, the CLT helps in determining whether a manufacturing process is consistent over time.

8. Pollsters use the CLT to predict election outcomes by sampling a small portion of the population.

9. Financial analysts apply the CLT to model stock prices and returns, assuming that the average of many small, random changes will be normally distributed.

Conditions for the Central Limit Theorem

Certain conditions must be met for the CLT to hold true. These conditions ensure the theorem's accuracy and reliability.

10. The sample size should be sufficiently large, typically n > 30, to approximate a normal distribution.

11. The samples must be independent, meaning the selection of one sample does not influence another.

12. The population from which samples are drawn should have a finite variance.

Variations of the Central Limit Theorem

There are different versions of the CLT that apply under various circumstances. These variations extend the theorem's applicability.

13. The Lindeberg-Feller CLT generalizes the theorem to cases where the random variables are not identically distributed.

14. The Lyapunov CLT provides conditions under which the theorem holds for sums of independent random variables with different distributions.

15. The Multivariate CLT extends the theorem to vectors of random variables, allowing for the study of multiple variables simultaneously.

Misconceptions about the Central Limit Theorem

Despite its importance, there are common misconceptions about the CLT. Clarifying these can help in better understanding the theorem.

16. One misconception is that the CLT only applies to normally distributed populations. In reality, it applies to any population distribution.

17. Another misconception is that a small sample size is sufficient for the CLT to hold. A larger sample size is generally required for accurate approximation.

18. Some believe the CLT guarantees a perfect normal distribution. It only approximates normality, especially with larger sample sizes.

Importance of the Central Limit Theorem in Research

The CLT plays a vital role in research, enabling scientists to draw conclusions from sample data.

19. In medical research, the CLT helps in determining the effectiveness of new treatments by analyzing sample data from clinical trials.

20. Environmental scientists use the CLT to study pollution levels by sampling air or water quality over time.

21. Social scientists rely on the CLT to understand human behavior by analyzing survey data from a subset of the population.

Central Limit Theorem in Machine Learning

Machine learning algorithms often rely on statistical principles, including the CLT, for accurate predictions and model training.

22. The CLT helps in understanding the distribution of errors in machine learning models, leading to better model evaluation.

23. It aids in the development of ensemble methods, where multiple models are combined to improve prediction accuracy.

24. The theorem is used in feature scaling, ensuring that data is normalized and follows a standard distribution for better model performance.

Real-World Examples of the Central Limit Theorem

Examples from everyday life illustrate the practical significance of the CLT.

25. Casino games, such as roulette, rely on the CLT to ensure that the house edge remains consistent over many plays.

26. In sports, the CLT helps in predicting team performance by analyzing player statistics over multiple games.

27. Weather forecasting uses the CLT to predict future conditions based on historical weather data.

Challenges and Limitations of the Central Limit Theorem

While powerful, the CLT has its challenges and limitations that must be considered.

28. The theorem assumes that samples are independent, which may not always be the case in real-world data.

29. The CLT may not hold for small sample sizes, leading to inaccurate approximations and predictions.

The Power of Central Limit Theorem

The Central Limit Theorem (CLT) is a cornerstone of statistics. It tells us that, regardless of the original distribution, the distribution of sample means will approach a normal distribution as the sample size grows. This principle is crucial for making inferences about populations from samples. It underpins many statistical methods, including hypothesis testing and confidence intervals.

Understanding CLT helps in fields like economics, psychology, and engineering. It allows researchers to make predictions and decisions based on sample data. The theorem simplifies complex data sets, making them easier to analyze and interpret.

In essence, the Central Limit Theorem bridges the gap between raw data and meaningful conclusions. It’s a powerful tool that transforms how we understand and utilize data in various disciplines. Embrace the CLT, and you’ll unlock a deeper understanding of the world through statistics.