25 Facts About Compactness

What is Compactness?

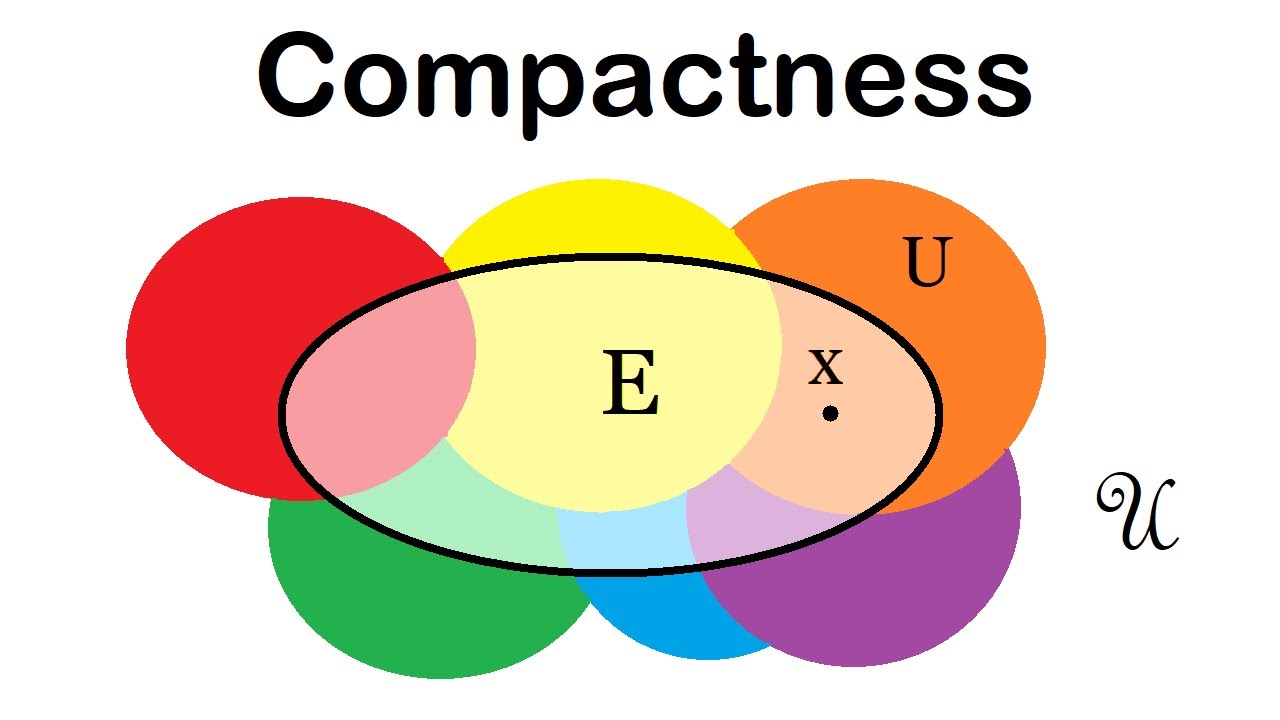
Compactness is a concept in mathematics, particularly in topology and analysis. It describes a space where every open cover has a finite subcover. This idea might sound complex, but it has practical applications in various fields. Let's explore some fascinating facts about compactness.

1. Origin of the Concept
   The idea of compactness was introduced by Maurice Fréchet in 1906. It has since become a fundamental concept in topology and analysis.

2. Heine-Borel Theorem
   The Heine-Borel Theorem states that a subset of Euclidean space is compact if and only if it is closed and bounded. This theorem is crucial in real analysis.

3. Finite Subcover
   A space is compact if every open cover has a finite subcover. This means you can cover the entire space with a finite number of open sets.

4. Sequential Compactness
   In metric spaces, compactness is equivalent to sequential compactness. This means every sequence has a convergent subsequence.

5. Bolzano-Weierstrass Theorem
   The Bolzano-Weierstrass Theorem states that every bounded sequence in (mathbb{R}^n) has a convergent subsequence. This is a direct consequence of compactness.

Applications of Compactness

Compactness isn't just a theoretical concept; it has practical applications in various fields, from physics to computer science.

6. Optimization Problems
   Compactness is used in optimization problems to ensure the existence of maximum and minimum values.

7. Quantum Mechanics
   In quantum mechanics, compact operators play a significant role in the study of quantum states and observables.

8. Computer Graphics
   Compactness helps in computer graphics for efficient rendering and storage of graphical data.

9. Economics
   In economics, compactness is used in fixed-point theorems, which are essential for proving the existence of equilibrium states.

10. Dynamical Systems
    Compactness is crucial in the study of dynamical systems, particularly in understanding the long-term behavior of systems.

Properties of Compact Spaces

Compact spaces have unique properties that make them interesting and useful in various mathematical contexts.

11. Closed Subsets
    Every closed subset of a compact space is also compact. This property is useful in many proofs and applications.

12. Continuous Functions
    Continuous functions on compact spaces are bounded and attain their maximum and minimum values. This is known as the Extreme Value Theorem.

13. Product of Compact Spaces
    The product of two compact spaces is also compact. This property is essential in product topology.

14. Compactness in Metric Spaces
    In metric spaces, compactness implies completeness and total boundedness. These properties are useful in analysis.

15. Compact Operators
    Compact operators on Hilbert spaces have discrete spectra, which is important in functional analysis.

Compactness in Different Contexts

Compactness can be understood differently depending on the context, such as in metric spaces, topological spaces, and functional analysis.

16. Compactness in Metric Spaces
    In metric spaces, compactness is equivalent to sequential compactness. This means every sequence has a convergent subsequence.

17. Compactness in Topological Spaces
    In topological spaces, compactness is defined using open covers. A space is compact if every open cover has a finite subcover.

18. Compactness in Functional Analysis
    In functional analysis, compact operators are those that map bounded sets to relatively compact sets.

19. Compactness in Algebraic Geometry
    In algebraic geometry, compactness is related to the concept of projective varieties, which are compact in the Zariski topology.

20. Compactness in Differential Geometry
    In differential geometry, compact manifolds are those that are closed and bounded. These manifolds have interesting topological properties.

Interesting Facts about Compactness

Compactness has some surprising and interesting aspects that make it a fascinating topic in mathematics.

21. Tychonoff's Theorem
    Tychonoff's Theorem states that the product of any collection of compact spaces is compact. This theorem is a cornerstone of topology.

22. Compactness and Connectedness
    A compact, connected metric space is path-connected. This means there is a continuous path between any two points in the space.

23. Compactness in Infinite Dimensions
    In infinite-dimensional spaces, compactness can be more complex. For example, the unit ball in an infinite-dimensional Hilbert space is not compact.

24. Compactness and Measure Theory
    In measure theory, compact sets have finite measure. This property is useful in integration and probability theory.

25. Compactness and Topological Groups
    In topological groups, compactness is related to the concept of compact Lie groups, which have applications in physics and representation theory.

Final Thoughts on Compactness

Compactness isn't just a buzzword; it’s a game-changer. From urban planning to technology, it shapes how we live and interact. Think about your smartphone—packed with features yet fits in your pocket. That’s compactness at work. In cities, compact design means more green spaces and less commuting time. It’s about making the most of what we have without wasting space or resources.

Understanding compactness helps us appreciate the efficiency in everyday objects and systems. It’s not just about size but about smart design and functionality. So next time you marvel at a tiny gadget or a well-planned city, remember the power of compactness. It’s all around us, making life easier and more efficient. Embrace it, and you’ll start seeing the world a bit differently.