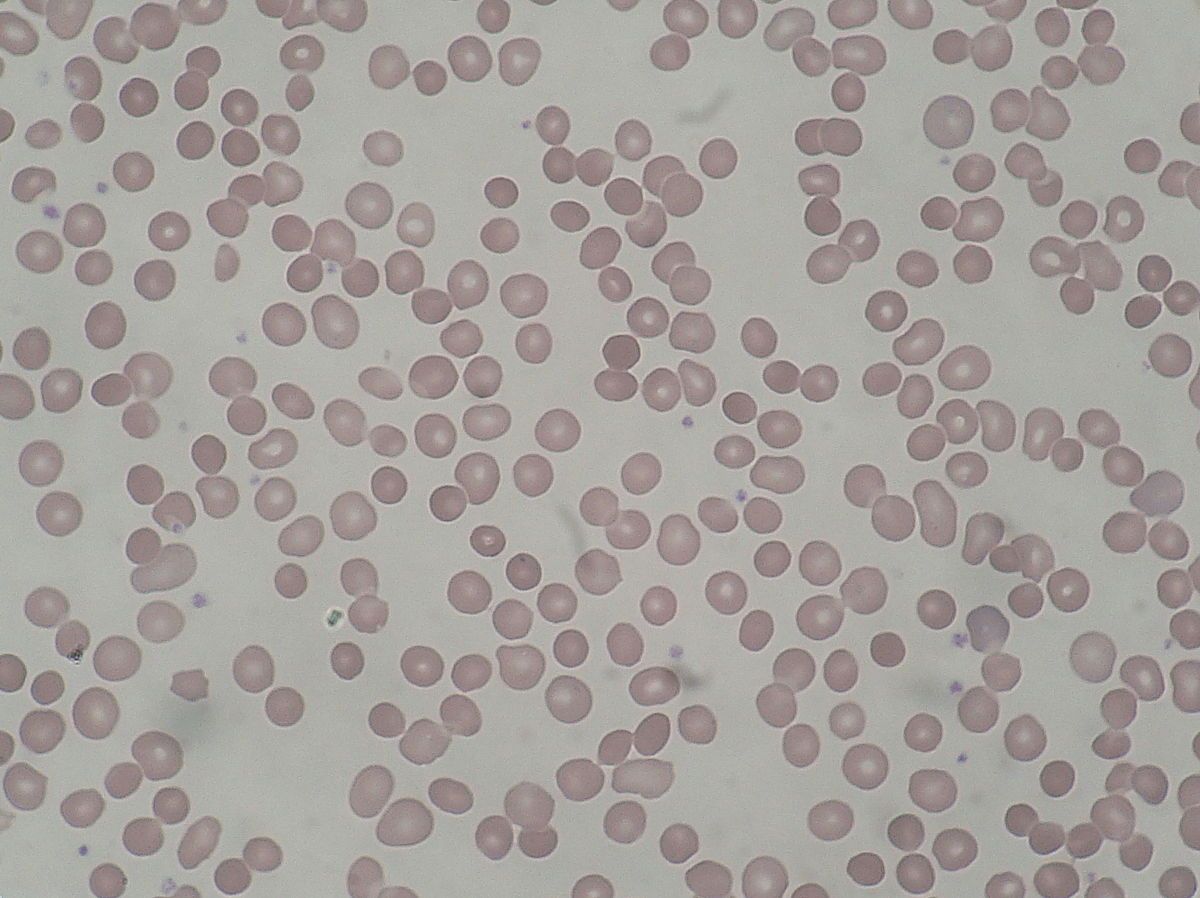
What is Minkowski–Chauffard syndrome? This rare genetic disorder, also known as hereditary spherocytosis, affects the red blood cells. Imagine tiny, round cells instead of the usual disc shape. These cells are more fragile and can break easily, leading to anemia. Symptoms might include fatigue, jaundice, and an enlarged spleen. It's like your body is working overtime to keep up with the broken cells. This condition is inherited, meaning it runs in families. If one parent has it, there's a chance their child might too. Treatment often involves managing symptoms, and sometimes removing the spleen helps. Understanding this syndrome can help those affected live healthier lives.
Key Takeaways:
- The Minkowski–Chauffard theorem connects shapes and numbers, influencing fields like cryptography, computer science, and physics. It's like a secret code that unlocks the hidden connections in math!
- This theorem is like a superhero, helping mathematicians solve complex problems and understand patterns in everything from economics to robotics. It's the key to unlocking mathematical mysteries!
Minkowski–Chauffard: A Mathematical Marvel
The Minkowski–Chauffard theorem is a fascinating topic in mathematics, particularly in the field of geometry and number theory. This theorem connects various mathematical concepts and has intriguing applications. Let's explore some interesting facts about this theorem.
-
Named After Two Mathematicians
The theorem is named after Hermann Minkowski and Émile Chauffard. Minkowski was a German mathematician known for his work in number theory and geometry, while Chauffard was a French mathematician who contributed to the development of this theorem. -
Part of Geometry and Number Theory
This theorem is a crucial part of both geometry and number theory. It provides insights into the relationships between geometric shapes and numbers, making it a bridge between these two mathematical fields. -
Involves Convex Bodies
The theorem deals with convex bodies, which are shapes where any line segment connecting two points within the shape lies entirely inside the shape. Convex bodies are fundamental in understanding the theorem's implications. -
Lattice Points Connection
Minkowski–Chauffard theorem has a significant connection with lattice points. Lattice points are points with integer coordinates, and the theorem helps in understanding how these points relate to convex bodies. -
Used in Optimization Problems
This theorem is often used in optimization problems, where the goal is to find the best solution from a set of possible solutions. It helps in determining the optimal arrangement of shapes and numbers. -
Applications in Cryptography
The principles of the Minkowski–Chauffard theorem are applied in cryptography, the science of securing communication. It aids in developing algorithms that protect data from unauthorized access. -
Influences Modern Mathematics
The theorem has influenced modern mathematics by providing a foundation for further research and discoveries. Its principles are used in various mathematical theories and applications. -
Involves Volume Calculations
Volume calculations are a key aspect of the theorem. It helps in determining the volume of convex bodies and their relationship with lattice points. -
Connected to Minkowski's Theorem
Minkowski–Chauffard theorem is closely related to Minkowski's theorem, which is another important result in geometry and number theory. Both theorems share similar principles and applications. -
Used in Computer Science
In computer science, the theorem is used in algorithms and data structures. It helps in optimizing processes and improving computational efficiency. -
Aids in Understanding Symmetry
The theorem provides insights into symmetry, a fundamental concept in mathematics. It helps in understanding how shapes and numbers exhibit symmetrical properties. -
Part of Mathematical Education
The theorem is often included in advanced mathematical education. It is taught in courses related to geometry, number theory, and optimization. -
Involves Linear Algebra
Linear algebra plays a role in the theorem, as it involves calculations related to vectors and matrices. Understanding linear algebra is essential for grasping the theorem's concepts. -
Helps in Solving Equations
The theorem aids in solving complex equations, particularly those involving geometric shapes and lattice points. It provides a framework for finding solutions to these equations. -
Used in Physics
In physics, the theorem is used to model and analyze physical phenomena. It helps in understanding the geometric properties of physical systems. -
Influences Engineering
Engineering applications often use the theorem to optimize designs and processes. It helps in creating efficient and effective engineering solutions. -
Part of Mathematical Research
The theorem is a subject of ongoing mathematical research. Mathematicians continue to explore its implications and applications in various fields. -
Involves Inequalities
Inequalities are a key component of the theorem. It helps in understanding the relationships between different mathematical quantities. -
Used in Economics
Economics uses the theorem to model and analyze economic systems. It helps in understanding the geometric properties of economic data. -
Connected to Geometry of Numbers
The theorem is part of the geometry of numbers, a branch of mathematics that studies the relationships between numbers and geometric shapes. -
Helps in Data Analysis
Data analysis often uses the theorem to interpret and analyze data. It helps in understanding the geometric properties of data sets. -
Part of Mathematical Competitions
The theorem is sometimes included in mathematical competitions. It challenges participants to apply its principles to solve complex problems. -
Involves Calculus
Calculus plays a role in the theorem, as it involves calculations related to rates of change and accumulation. Understanding calculus is essential for grasping the theorem's concepts. -
Used in Architecture
Architecture uses the theorem to design and analyze structures. It helps in understanding the geometric properties of architectural designs. -
Aids in Understanding Patterns
The theorem provides insights into patterns, a fundamental concept in mathematics. It helps in understanding how shapes and numbers exhibit patterned properties. -
Part of Mathematical Software
Mathematical software often includes the theorem as part of its algorithms and calculations. It helps in optimizing processes and improving computational efficiency. -
Involves Probability
Probability plays a role in the theorem, as it involves calculations related to likelihood and uncertainty. Understanding probability is essential for grasping the theorem's concepts. -
Used in Robotics
Robotics uses the theorem to model and analyze robotic systems. It helps in understanding the geometric properties of robotic designs. -
Connected to Algebraic Geometry
The theorem is part of algebraic geometry, a branch of mathematics that studies the relationships between algebraic equations and geometric shapes. -
Helps in Understanding Complexity
The theorem provides insights into complexity, a fundamental concept in mathematics. It helps in understanding how shapes and numbers exhibit complex properties.
Final Thoughts on Minkowski–Chauffard
Minkowski–Chauffard syndrome, also known as hereditary spherocytosis, is a genetic disorder affecting the red blood cells. These cells become sphere-shaped, leading to their premature destruction. This condition often results in anemia, jaundice, and an enlarged spleen. Treatment usually involves managing symptoms, and in severe cases, a splenectomy might be necessary to improve quality of life.
Understanding the genetic basis of this syndrome helps in early diagnosis and better management. Genetic counseling can be beneficial for families with a history of the disorder. While it might sound complex, the key takeaway is that with proper medical care, individuals with Minkowski–Chauffard can lead healthy lives.
Stay informed and consult healthcare professionals for personalized advice. Knowledge is power, and being aware of such conditions can make a significant difference in managing health effectively.
Frequently Asked Questions
Was this page helpful?
Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.
